Sử dụng kiến thức về số trung bình của mẫu số liệu để tính. Hướng dẫn giải Giải bài 5 trang 162 sách bài tập toán 11 – Chân trời sáng tạo tập 1 – Bài tập cuối chương 5. Kết quả điều tra về số giờ làm thêm trong một tuần của 100 sinh viên được cho ở biểu…
Đề bài/câu hỏi:
Kết quả điều tra về số giờ làm thêm trong một tuần của 100 sinh viên được cho ở biểu đồ bên.
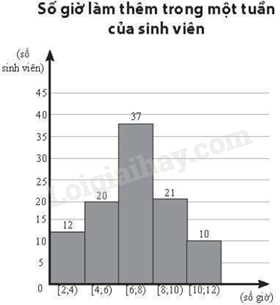
Hãy ước lượng số trung bình, mốt và các tứ phân vị của mẫu số liệu đó.
Hướng dẫn:
+ Sử dụng kiến thức về số trung bình của mẫu số liệu để tính:
Giả sử mẫu số được cho dưới dạng bảng tần số ghép nhóm:

Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính như sau: \(\overline x = \frac{{{n_1}{c_1} + {n_2}{c_2} + … + {n_k}{c_k}}}{n}\), trong đó \(n = {n_1} + {n_2} + … + {n_k}\).
+ Sử dụng kiến thức về mốt của mẫu số liệu để tính: Giả sử nhóm chứa mốt là \(\left[ {{u_m};{u_{m + 1}}} \right)\), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là \({M_O}\) được xác định bởi công thức: \({M_O} = {u_m} + \frac{{{n_m} – {n_{m – 1}}}}{{\left( {{n_m} – {n_{m – 1}}} \right) + \left( {{n_m} – {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} – {u_m}} \right)\)
+ Sử dụng kiến thức xác định trung vị của mẫu số liệu ghép nhóm để tính:
Gọi n là cỡ mẫu.
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa trung vị, \({n_m}\) là tần số của nhóm chứa trung vị,
\(C = {n_1} + {n_2} + … + {n_{m – 1}}\).
Khi đó, trung vị của mẫu số liệu là: \({M_e} = {u_m} + \frac{{\frac{n}{2} – C}}{{{n_m}}}.\left( {{u_{m + 1}} – {u_m}} \right)\).
+ Sử dụng kiến thức về xác định tứ phân vị của mẫu số liệu ghép nhóm để tính:
Tứ phân vị thứ hai của mẫu số liệu ghép nhóm, kí hiệu \({Q_2}\), cũng chính là trung vị của mẫu số liệu ghép nhóm.
Để tìm tứ phân vị thứ nhất của mẫu số liệu ghép nhóm, kí hiệu \({Q_1}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa tứ phân vị thứ nhất, \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ nhất, \(C = {n_1} + {n_2} + … + {n_{m – 1}}\)
Khi đó, tứ phân vị thứ nhất của mẫu số liệu là: \({Q_1} = {u_m} + \frac{{\frac{n}{4} – C}}{{{n_m}}}.\left( {{u_{m + 1}} – {u_m}} \right)\)
Để tìm tứ phân vị thứ ba của mẫu số liệu ghép nhóm, kí hiệu \({Q_3}\), ta làm như sau:
Giả sử nhóm \(\left[ {{u_j};{u_{j + 1}}} \right)\) chứa tứ phân vị thứ ba, \({n_j}\) là tần số của nhóm chứa tứ phân vị thứ ba, \(C = {n_1} + {n_2} + … + {n_{j – 1}}\)
Khi đó, tứ phân vị thứ ba của mẫu số liệu là: \({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} – C}}{{{n_j}}}.\left( {{u_{j + 1}} – {u_j}} \right)\)
Lời giải:
Ta có bảng tần số ghép nhóm gồm các giá trị đại diện của nhóm là:

Cỡ mẫu \(n = 100\)
Số trung bình của mẫu số liệu là: \(\overline x = \frac{{12.3 + 20.5 + 37.7 + 21.9 + 11.10}}{{100}} = 6,94\)
Nhóm chứa mốt của mẫu số liệu là \(\left[ {6;8} \right)\).
Do đó, \({u_m} = 6,{u_{m + 1}} = 8,{n_m} = 37,{n_{m + 1}} = 20,{u_{m + 1}} – {u_m} = 8 – 6 = 2\)
Mốt của mẫu số liệu là: \({M_O} = 6 + \frac{{37 – 20}}{{\left( {37 – 20} \right) + \left( {37 – 21} \right)}}.2 = \frac{{232}}{{33}}\)
Gọi \({x_1},{x_2},…,{x_{100}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Ta có: \({x_1},…,{x_{12}} \in \left[ {2;4} \right),{x_{13}},…,{x_{32}} \in \left[ {4;6} \right),{x_{33}},…,{x_{69}} \in \left[ {6;8} \right),\) \({x_{70}},…,{x_{90}} \in \left[ {8;10} \right),{x_{90}},…,{x_{100}} \in \left[ {10;12} \right)\).
Do cỡ mẫu \(n = 100\) nên tứ phân vị thứ hai của mẫu số liệu là \(\frac{1}{2}\left( {{x_{50}} + {x_{51}}} \right)\). Do đó tứ phân vị thứ hai của mẫu số liệu thuộc nhóm \(\left[ {6;8} \right)\).
Tứ phân vị thứ hai của mẫu số liệu ghép nhóm là:\({Q_2} = 6 + \frac{{\frac{{100}}{2} – \left( {12 + 20} \right)}}{{37}}.\left( {8 – 6} \right) = \frac{{258}}{{37}}\)
Do cỡ mẫu \(n = 100\) nên tứ phân vị thứ nhất của mẫu số liệu là \(\frac{1}{2}\left( {{x_{25}} + {x_{26}}} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm \(\left[ {4;6} \right)\).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 4 + \frac{{\frac{{100}}{4} – 12}}{{20}}.\left( {6 – 4} \right) = 5,3\)
Do cỡ mẫu \(n = 100\) nên tứ phân vị thứ ba của mẫu số liệu là \(\frac{1}{2}\left( {{x_{75}} + {x_{76}}} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu thuộc nhóm \(\left[ {8;10} \right)\).
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_3} = 8 + \frac{{\frac{{3.100}}{4} – \left( {12 + 20 + 37} \right)}}{{21}}.\left( {10 – 8} \right) = \frac{{60}}{7}\)