Sử dụng kiến thức về góc giữa đường thẳng và mặt phẳng để tính. Giải và trình bày phương pháp giải Giải bài 3 trang 76 sách bài tập toán 11 – Chân trời sáng tạo tập 2 – Bài tập cuối chương 8. Cho hình chóp S. ABC có đáy là tam giác đều cạnh a….
Đề bài/câu hỏi:
Cho hình chóp S. ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho \(HA = 2HB\). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng \({60^0}\). Tính khoảng cách giữa hai đường thẳng SA và BC theo a.
Hướng dẫn:
– Sử dụng kiến thức về góc giữa đường thẳng và mặt phẳng để tính:
+ Nếu đường thẳng a vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a với (P) bằng \({90^0}\).
+ Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa đường thẳng a và hình chiếu a’ của a trên (P) gọi là góc giữa đường thẳng a và (P).
– Sử dụng kiến thức về khoảng cách giữa hai đường thẳng chéo nhau để tính: Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó, kí hiệu d(a, b).
Lời giải:
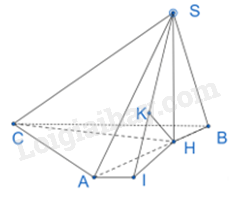
Áp dụng định lí côsin vào tam giác AHC có:
\(C{H^2} \) \( = A{C^2} + A{H^2} – 2AC.AH.\cos \widehat {CAH}\)
\( \Rightarrow C{H^2} \) \( = {a^2} + {\left( {\frac{{2a}}{3}} \right)^2} – 2a.\frac{{2a}}{3}.\cos {60^0} \) \( = \frac{{7{a^2}}}{9} \Rightarrow CH \) \( = \frac{{a\sqrt 7 }}{3}\)
Vì \(SH \bot \left( {ABC} \right)\) nên HC là hình chiếu vuông góc của SC trên mặt phẳng (ABC)
Do đó, \(\left( {SC,\left( {ABC} \right)} \right) \) \( = \left( {SC,HC} \right) \) \( = \widehat {SCH} \) \( = {60^0}\)
Trong tam giác SCH vuông tại H có: \(SH \) \( = CH.\tan {60^0} \) \( = \frac{{a\sqrt 7 }}{3}.\sqrt 3 \) \( = \frac{{a\sqrt {21} }}{3}\)
Qua A kẻ đường thẳng song song với BC, I là hình chiếu của H trên đường thẳng đó.
Khi đó, BC//AI. Suy ra: \(d\left( {BC,SA} \right) \) \( = d\left( {BC,\left( {SAI} \right)} \right) \) \( = d\left( {B,\left( {SAI} \right)} \right) \) \( = \frac{3}{2}d\left( {H;\left( {SAI} \right)} \right)\)
Gọi K là hình chiếu của H trên SI.
Vì \(SH \bot AI,AI \bot HI \Rightarrow AI \bot \left( {SHI} \right) \Rightarrow AI \bot KH\)
Mà \(HK \bot SI \Rightarrow HK \bot \left( {SAI} \right) \Rightarrow d\left( {H,\left( {SAI} \right)} \right) \) \( = HK\)
Ta có: \(\widehat {HAI} \) \( = {180^0} – \left( {{{60}^0} + {{60}^0}} \right) \) \( = {60^0}\)
Tam giác AHI vuông tại I nên \(HI \) \( = HA.\sin {60^0} \) \( = \frac{{2a}}{3}.\frac{{\sqrt 3 }}{2} \) \( = \frac{{a\sqrt 3 }}{3}\)
Tam giác SIH vuông tại H có: \(\frac{1}{{H{K^2}}} \) \( = \frac{1}{{H{S^2}}} + \frac{1}{{H{I^2}}} \) \( = \frac{9}{{21{a^2}}} + \frac{9}{{3{a^2}}} \) \( = \frac{{24}}{{7{a^2}}} \Rightarrow HK \) \( = \frac{{a\sqrt {42} }}{{12}}\)
Do đó: \(d\left( {BC,SA} \right) \) \( = \frac{{a\sqrt {42} }}{8}\)