Sử dụng kiến thức về giới hạn một phía để tính: + Cho \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = L. Lời giải Giải bài 12 trang 85 sách bài tập toán 11 – Chân trời sáng tạo tập 1 – Bài 2. Giới hạn của hàm số. Trong mặt phẳng tọa độ Oxy, cho điểm \(M\left( {t,{t^2}} \right),t > 0\), nằm trên đường parabol \(y = {x^2}\)….
Đề bài/câu hỏi:
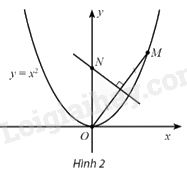
Trong mặt phẳng tọa độ Oxy, cho điểm \(M\left( {t,{t^2}} \right),t > 0\), nằm trên đường parabol \(y = {x^2}\). Đường trung trực của đoạn thẳng OM cắt trục tung tại N. Điểm N dần đến điểm nào khi M dần đến điểm O?
Hướng dẫn:
Sử dụng kiến thức về giới hạn một phía để tính:
+ Cho \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = L,\mathop {\lim }\limits_{x \to x_0^ + } g\left( x \right) = M\), khi đó: \(\mathop {\lim }\limits_{x \to x_0^ + } \left[ {f\left( x \right) + g\left( x \right)} \right] = L + M\)
+ \(\mathop {\lim }\limits_{x \to x_0^ + } c = c\) (với c là hằng số).
Lời giải:
Trung điểm của đoạn thẳng OM là \(I\left( {\frac{t}{2};\frac{{{t^2}}}{2}} \right)\)
Đường trung trực của OM nhận vectơ \(\overrightarrow {OM} = \left( {t,{t^2}} \right)\) làm vectơ pháp tuyến nên có phương trình d: \(t\left( {x – \frac{t}{2}} \right) + {t^2}\left( {y – \frac{{{t^2}}}{2}} \right) = 0\).
Thay \(x = 0\) vào phương trình của d, ta nhận được \(y = \frac{1}{2}\left( {1 + {t^2}} \right)\)
Suy ra \(N\left( {0;\frac{1}{2}\left( {1 + {t^2}} \right)} \right)\).
Điểm M dần đến điểm O khi t dần đến \({0^ + }\). Ta có: \(\mathop {\lim }\limits_{t \to {0^ + }} \frac{1}{2}\left( {1 + {t^2}} \right) = \frac{1}{2}\left( {1 + {0^2}} \right) = \frac{1}{2}\).
Suy ra điểm M dần đến điểm O khi điểm N dần đến điểm \(A\left( {0;\frac{1}{2}} \right)\).