Áp dụng các công thức đã học để xác định các đại lượng tiêu biểu. Lời giải Giải bài 4 trang 9, 10 sách bài tập toán 11 – Cánh diều – Bài 1. Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm. Khi thống kê chỉ số đường huyết (đơn vị: mmol/L) của 28 người cao tuổi trong một lần đo,…
Đề bài/câu hỏi:
Khi thống kê chỉ số đường huyết (đơn vị: mmol/L) của 28 người cao tuổi trong một lần đo, ta được kết quả sau:

a) Lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy có năm nhóm ứng với năm nửa khoảng: [7,0;7,2), [7,2;7,4), [7,4;7,6), [7,6;7,8), [7,8;8,0].
b) Độ dài của mỗi nhóm bằng:
A. 7.
B. 8.
C. 1.
D. 0,2.
c) Tần số của nhóm [7,8;8,0] là bao nhiêu?
A. 3.
B. 5.
C. 6.
D. 7.
d) Giá trị \(c{f_3}\) bằng:
A. 7.
B. 13.
C. 20.
D. 25.
e) Giá trị đại diện của nhóm [7,4;7,6) bằng:
A. 7,4.
B. 7,6.
C. 7,5.
D. 2.
g) Nhóm có giá trị đại diện bằng 7,7 là:
A. [7,0;7,2).
B. [7,2;7,4).
C. [7,4;7,6).
D. [7,6;7,8).
Hướng dẫn:
Áp dụng các công thức đã học để xác định các đại lượng tiêu biểu.
Lời giải:
a) Bảng tần số ghép nhóm cho mẫu số liệu có năm nhóm ứng với năm nửa khoảng:
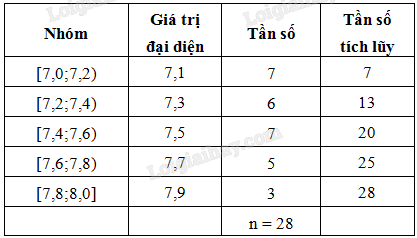
b) Độ dài của mỗi nhóm bằng: 0,2.
Đáp án D.
c) Tần số của nhóm [7,8;8,0] là 3.
Đáp án A.
d) Giá trị \(c{f_3}\) bằng: 20.
Đáp án C.
e) Giá trị đại diện của nhóm [7,4;7,6) bằng: 7,5.
Đáp án C.
g) Nhóm có giá trị đại diện bằng 7,7 là: [7,6;7,8).
Đáp án D.