Chỉ ra hàm số không xác định tại \(x = \frac{5}{3}\), từ đó kết luận hàm số không liên tục tại \(x = \frac{5}{3}\). Lời giải Giải bài 28 trang 81 sách bài tập toán 11 – Cánh diều – Bài 3. Hàm số liên tục. Quan sát đồ thị hàm số trong hình dưới đây và cho biết hàm số đó có liên tục:…
Đề bài/câu hỏi:
Quan sát đồ thị hàm số trong hình dưới đây và cho biết hàm số đó có liên tục:
a) Tại \(x = \frac{5}{3}\) hay không.
b) Trên khoảng \(\left( { – \infty ;0} \right)\) hay không.
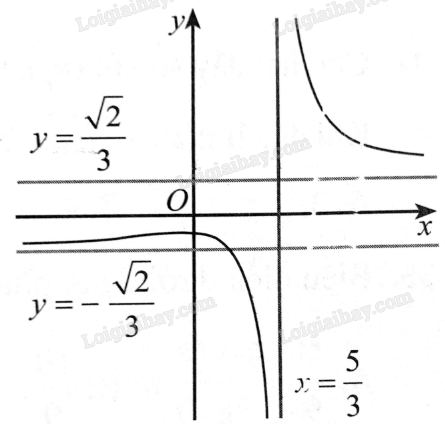
Hướng dẫn:
a) Chỉ ra hàm số không xác định tại \(x = \frac{5}{3}\), từ đó kết luận hàm số không liên tục tại \(x = \frac{5}{3}\).
b) Chỉ ra rằng đồ thị hàm số trên khoảng \(\left( { – \infty ,0} \right)\) là “đường liền”, từ đó suy ra hàm số liên tục trên \(\left( { – \infty ,0} \right)\).
Lời giải:
a) Từ đồ thị, ta nhận thấy rằng không có giá trị của hàm số tại \(x = \frac{5}{3}\), tức là hàm số không xác định tại \(x = \frac{5}{3}\). Như vậy hàm số không liên tục tại \(x = \frac{5}{3}\).
b) Từ đồ thị, ta nhận thấy trên khoảng \(\left( { – \infty ,0} \right)\), đồ thị hàm số là một “đường liền”. Do đó, hàm số liên tục trên khoảng \(\left( { – \infty ,0} \right)\).