Vẽ hình, chỉ ra góc \(\alpha \) và \(\beta \) trên hình vẽ rồi so sánh chúng. Giải và trình bày phương pháp giải Giải bài 26 trang 99 sách bài tập toán 11 – Cánh diều – Bài 3. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện. Cho hình chóp (S.ABC) có (SA bot left( {ABC} right))….
Đề bài/câu hỏi:
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\). Gọi \(I\) là hình chiếu của \(A\) trên đường thẳng \(BC\), \(\alpha \) là góc giữa đường thẳng \(SI\) và mặt phẳng \(\left( {ABC} \right)\), \(\beta \) là số đo của góc nhị diện \(\left[ {S,BC,A} \right]\). Phát biểu nào sau đây là đúng?
A. \(\alpha = {90^o} – \beta \)
B. \(\alpha = {180^o} – \beta \)
C. \(\alpha = {90^o} + \beta \)
D. \(\alpha = \beta \)
Hướng dẫn:
Vẽ hình, chỉ ra góc \(\alpha \) và \(\beta \) trên hình vẽ rồi so sánh chúng.
Lời giải:
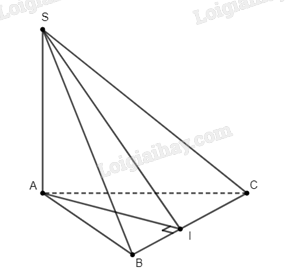
Do \(SA \bot \left( {ABC} \right)\), ta suy ra hình chiếu của \(S\) trên \(\left( {ABC} \right)\) là điểm \(A\).
Suy ra góc giữa \(SI\) và \(\left( {ABC} \right)\) chính là góc \(\widehat {SIA}\), tức là \(\alpha = \widehat {SIA}\).
Mặt khác, do \(SA \bot \left( {ABC} \right)\), ta suy ra \(SA \bot BC\). Mà theo đề bài, \(AI \bot BC\) nên ta suy ra \(\left( {SAI} \right) \bot BC\), từ đó \(SI \bot BC\).
Như vậy, do \(SI \bot BC\), \(AI \bot BC\), nên \(\widehat {SIA}\) chính là góc phẳng nhị diện của góc nhị diện \(\left[ {S,BC,A} \right]\), tức là \(\beta = \widehat {SIA}\).
Vậy ta suy ra \(\alpha = \beta \).
Đáp án đúng là D.