Giải Luyện tập Bài 5. Phép dời hình (trang 21, 22, 23) – Chuyên đề học tập Toán 11 Kết nối tri thức. Tham khảo: Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy.
Câu hỏi/Đề bài:
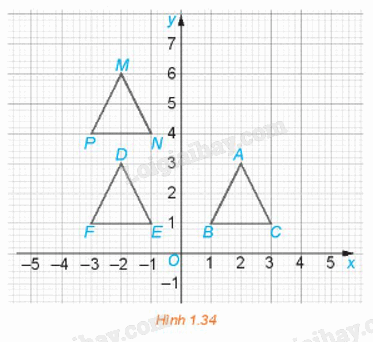
Trong mặt phẳng tọa độ Oxy ở Hình 1.34, gọi f là phép biến hình biến mỗi điểm có tọa độ \(\left( {x;{\rm{ }}y} \right)\) thành điểm có tọa độ \(\left( {-{\rm{ }}x;{\rm{ }}y{\rm{ }} + {\rm{ }}3} \right).\) Trong các khẳng định sau, những khẳng định nào đúng.
a) f biến \(\Delta \)ABC thành \(\Delta \)DEF.
b) f biến \(\Delta \)DEF thành \(\Delta \)MNP.
c) f biến \(\Delta \)ABC thành \(\Delta \)MNP.
Hướng dẫn:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M’ = f(M)\).
Lời giải:
Từ Hình 1.34, ta thấy: \(A\left( {2;{\rm{ }}3} \right),{\rm{ }}B\left( {1;{\rm{ }}1} \right),{\rm{ }}C\left( {3;{\rm{ }}1} \right),{\rm{ }}D\left( {-{\rm{ }}2;{\rm{ }}3} \right),{\rm{ }}E\left( {-{\rm{ }}1;{\rm{ }}1} \right),{\rm{ }}F\left( {-{\rm{ }}3;{\rm{ }}1} \right),{\rm{ }}M\left( {-{\rm{ }}2;{\rm{ }}6} \right),{\rm{ }}N\left( {-{\rm{ }}1;{\rm{ }}4} \right),{\rm{ }}P\left( {-{\rm{ }}3;{\rm{ }}4} \right).\)
+ Phép biến hình f biến điểm A(2; 3) thành điểm có tọa độ \(\left( {-{\rm{ }}2;{\rm{ }}3{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ }}\left( {-{\rm{ }}2;{\rm{ }}6} \right)\) hay chính là điểm M.
Phép biến hình f biến điểm B(1; 1) thành điểm có tọa độ \(\left( {-{\rm{ }}1;{\rm{ }}1{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ }}\left( {-{\rm{ }}1;{\rm{ }}4} \right)\) hay chính là điểm N.
Phép biến hình f biến điểm C(3; 1) thành điểm có tọa độ \(\left( {-{\rm{ }}3;{\rm{ }}1{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ }}\left( {-{\rm{ }}3;{\rm{ }}4} \right)\) hay chính là điểm P.
Do đó, phép biến hình f biến tam giác ABC thành tam giác MNP nên khẳng định c) đúng và khẳng định a) sai.
+ Phép biến hình f biến điểm D(- 2; 3) thành điểm có tọa độ \(\left( {-{\rm{ }}\left( {-{\rm{ }}2} \right);{\rm{ }}3{\rm{ }} + {\rm{ }}3} \right){\rm{ }} = {\rm{ }}\left( {2;{\rm{ }}6} \right).\)
Do đó, phép biến hình f không biến tam giác DEF thành tam giác MNP nên khẳng định b) sai.
Vậy trong các khẳng định đã cho, chỉ có khẳng định c) đúng.