Giải chi tiết Luyện tập 1 Bài 3. Phép đối xứng trục (trang 12, 13) – Chuyên đề học tập Toán 11 Kết nối tri thức. Gợi ý: Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M’}} = {x_M}\\{y_{M’}} = – {y_M}\end{array} \right. \.
Câu hỏi/Đề bài:
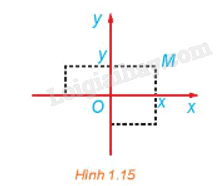
Xét mặt phẳng tọa độ Oxy (H.1.15). Trong các khẳng định sau, chọn các khẳng định đúng.
a) Phép đối xứng trục Ox biến mỗi điểm \(M\left( {x;{\rm{ }}y} \right)\) thành điểm có tọa độ \(\left( {x;{\rm{ }}-{\rm{ }}y} \right).\)
b) Phép đối xứng trục Oy biến mỗi điểm \(M\left( {x;{\rm{ }}y} \right)\) thành điểm có tọa độ \(\left( {-{\rm{ }}x;{\rm{ }}y} \right).\)
c) Phép đối xứng trục Ox biến A(1; 2) thành điểm \(A’\left( {-{\rm{ }}1;{\rm{ }}-{\rm{ }}2} \right).\)
Hướng dẫn:
Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M’}} = {x_M}\\{y_{M’}} = – {y_M}\end{array} \right.\)
Nếu thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M’}} = – {x_M}\\{y_{M’}} = {y_M}\end{array} \right.\)
Lời giải:
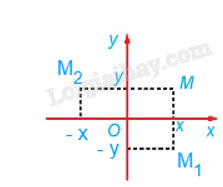
Từ hình vẽ ta thấy:
+) Phép đối xứng trục Ox biến mỗi điểm M(x; y) thành điểm M1(x; – y).
+) Phép đối xứng trục Oy biến mỗi điểm M(x; y) thành điểm M2(- x; y).
Do đó, phép đối xứng trục Ox biến điểm A(1; 2) thành A'(1; – 2).
Vậy các khẳng định a), b) đúng và khẳng định c) sai.