Bài 2.18 trang 49 Chuyên đề học tập Toán 11 Kết nối tri thức: Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.36

Đề bài/câu hỏi:

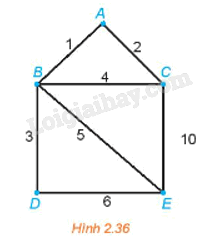
Giải bài toán người đưa thư đối với đồ thị có trọng số trên Hình 2.36.

Hướng dẫn:

Giải bài toán bằng thuật toán người đưa thư

Lời giải:

Đồ thị Hình 2.36 chỉ có hai đỉnh bậc lẻ là C và E nên ta có thể tìm được một đường đi Euler từ C đến E (đường đi này đi qua mỗi cạnh đúng một lần).

Một đường đi Euler từ đỉnh C đến đỉnh E là CABCEBDE và tổng độ dài của nó là

2 + 1 + 4 + 10 + 5 + 3 + 6 = 31.

Để quay trở lại điểm xuất phát và có đường đi ngắn nhất, ta cần tìm một đường đi ngắn nhất từ E đến C theo thuật toán gắn nhãn vĩnh viễn.

Đường đi ngắn nhất từ E đến C là EBAC và có độ dài là 5 + 1 + 2 = 8.

Vậy một chu trình cần tìm là CABCEBDEBAC và có độ dài là 31 + 8 = 39.