Bài 1.27 trang 33 Chuyên đề học tập Toán 11 Kết nối tri thức: Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ : 2x – y – 1 = 0 và hai điểm A – 1; 2

Đề bài/câu hỏi:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\Delta :{\rm{ }}2x{\rm{ }}-{\rm{ }}y{\rm{ }}-{\rm{ }}1{\rm{ }} = {\rm{ }}0\) và hai điểm \(A\left( {-{\rm{ }}1;{\rm{ }}2} \right),{\rm{ }}B\left( {-{\rm{ }}3;{\rm{ }}4} \right).\)

a) Tìm tọa độ điểm \(A’\) là ảnh của điểm A qua phép đối xứng trục \(\Delta \)

b) Xác định điểm M thuộc đường thẳng \(\Delta \) sao cho MA + MB đạt giá trị nhỏ nhất.

Hướng dẫn:

Dựa vào kiến thức đã học về phép đối xứng trục để làm

Lời giải:

a) Ta có: \(2{\rm{ }}.{\rm{ }}\left( {-{\rm{ }}1} \right){\rm{ }}-{\rm{ }}2{\rm{ }}-{\rm{ }}1{\rm{ }} = {\rm{ }}-{\rm{ }}5{\rm{ }} \ne {\rm{ }}0\) nên \(A\left( {-{\rm{ }}1;{\rm{ }}2} \right)\) không thuộc ∆.

Gọi H là chân đường vuông góc hạ từ A xuống ∆.

Vì H thuộc ∆ nên \(H\left( {x;2x-1} \right)\). Ta có: \(\overrightarrow {AH} = (x + 1;2x – 3)\), vectơ chỉ phương của đường thẳng ∆ là \(\overrightarrow {{u_\Delta }} = \left( {1;\,2} \right)\)

Vì AH vuông góc với ∆ nên \(\overrightarrow {AH} .\overrightarrow {{u_\Delta }} = 0 \Leftrightarrow \left( {x + 1} \right).1 + \left( {2x – 3} \right).2 = 0 \Rightarrow x = 1\)

Từ đó suy ra H(1; 1).

Vì A’ là ảnh của điểm A qua phép đối xứng trục ∆ nên AA’ vuông góc với ∆ tại H và H là trung điểm của AA’.

Suy ra \(\left\{ {\begin{array}{*{20}{l}}{{x_{A’}} = 2{x_H} – {x_A} = 2.1 – \left( { – 1} \right) = 3}\\{{y_{A’}} = 2{y_H} – {y_A} = 2.1 – 2 = 0}\end{array}} \right.\)

Vậy A'(3; 0).

b)

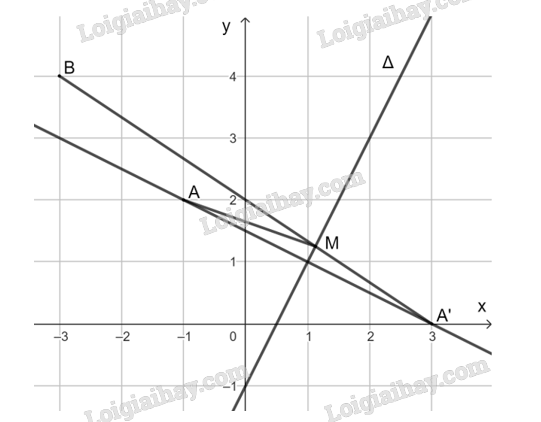
Ta có: \(2.\left( {-3} \right)-4-1{\rm{ }} = -11;{\rm{ 2}}.\left( {-1} \right)-2-1 = -5\) và \(\left( {-11} \right).\left( {-5} \right) = 55 > 0\)nên hai điểm A và B nằm về một phía của đường thẳng ∆.

Vì M thuộc \(\Delta \) và A và A’ đối xứng nhau qua \(\Delta \) nên MA = MA’ và A’ và B nằm về hai phía của đường thẳng \(\Delta \).

Do đó, MA + MB = MA’ + MB đạt giá trị nhỏ nhất khi M là giao điểm của A’B và \(\Delta \).

Ta có: \(\overrightarrow {A’B} = ( – 6;4)\), suy ra \(\overrightarrow {{n_{A’B}}} = (2;3)\) là một vectơ pháp tuyến của đường thẳng A’B. Phương trình đường thẳng A’B là \(2\left( {x-3} \right) + 3\left( {y-0} \right) = 0\) hay \(2x + 3y-6 = 0.\)

Tọa độ giao điểm M của A’B và ∆ là nghiệm của hệ phương trình

\(\left\{ {\begin{array}{*{20}{l}}{2x – y – 1 = 0}\\{2x + 3y – 6 = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = \frac{9}{8}}\\{y = \frac{5}{4}}\end{array}} \right.} \right.\)

Vậy \(M\left( {\frac{9}{8};\,\frac{5}{4}} \right)\).