Hướng dẫn giải Vận dụng 2 Bài 7. Phép đồng dạng (trang 39, 40) – Chuyên đề học tập Toán 11 Chân trời sáng tạo. Tham khảo: Quan sát hình 5 để tìm các cặp hình đồng dạng.
Câu hỏi/Đề bài:
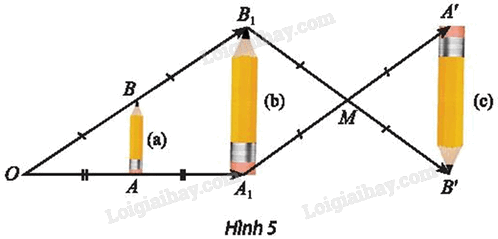
Tìm các cặp hình đồng dạng với nhau có trong Hình 5.
Hướng dẫn:
Quan sát hình 5 để tìm các cặp hình đồng dạng
Lời giải:
⦁ Xét cặp hình (a) và (b):
Ta có \(O{A_1}\; = {\rm{ }}2OA\) và \(\overrightarrow {O{A_1}} \; ,\,\overrightarrow {OA} \) cùng phương.
Suy ra \(\overrightarrow {O{A_1}} = 2\,\overrightarrow {OA} \)
Do đó \({V_{\left( {O,{\rm{ }}2} \right)}}\left( A \right){\rm{ }} = {\rm{ }}{A_1}.\)
Chứng minh tương tự, ta được \({V_{\left( {O,{\rm{ }}2} \right)}}\left( B \right){\rm{ }} = {\rm{ }}{B_1}.\)
Vì vậy \({V_{\left( {O,{\rm{ }}2} \right)}}\left( {AB} \right){\rm{ }} = {\rm{ }}{A_1}{B_1}.\)
Khi đó \({V_{\left( {O,{\rm{ }}2} \right)}}\;\) biến hình (a) thành hình (b).
Vì vậy phép đồng dạng tỉ số 2 biến hình (a) thành hình (b).
Do đó hình (a) và hình (b) đồng dạng với nhau.
⦁ Ta xét hình (b) và hình (c):
Ta có M là trung điểm B1B’.
Suy ra \(B'{\rm{ }} = {\rm{ }}{Đ_M}({B_1}).\)
Chứng minh tương tự, ta được \(A'{\rm{ }} = {\rm{ }}{Đ_M}({A_1}).\)
Do đó
Khi đó \({Đ_M}\) biến hình (b) thành hình (c).
Vì vậy phép đồng dạng tỉ số 1 biến hình (b) thành hình (c).
Do đó hình (b) và hình (c) đồng dạng với nhau.
⦁ Ta xét hình (a) và hình (c):
Ta có phép đồng dạng có được bằng cách thực hiện liên tiếp \({V_{\left( {O,{\rm{ }}2} \right)}}\;\) và \({Đ_M}\) biến hình (a) thành hình (c).
Do đó hình (a) và hình (c) đồng dạng với nhau.
Vậy các cặp hình đồng dạng với nhau có trong Hình 5 là: cặp hình (a) và (b); cặp hình (b) và (c); cặp hình (c) và (a).