Vận dụng 1 Bài 7 (trang 38, 39) Chuyên đề học tập Toán 11: Tìm phép đồng dạng biến hình (A) thành hình (C)

Câu hỏi/Đề bài:

Tìm phép đồng dạng biến hình (A) thành hình (C).

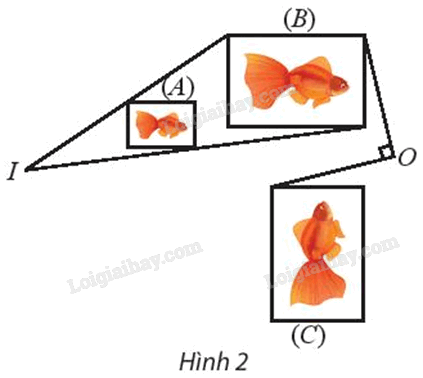
Hướng dẫn:

Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M’N’ = k.MN\)

Lời giải:

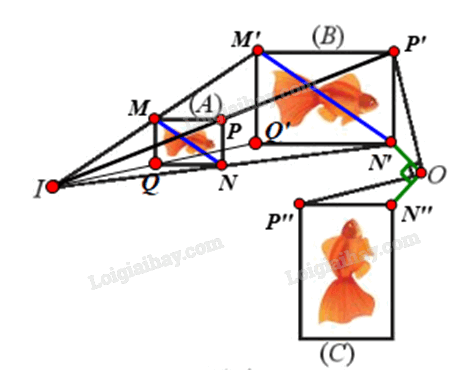
Gọi f là phép đồng dạng cần tìm.

⦁ Để tìm phép biến hình biến hình (A) thành hình (B), ta tìm phép biến hình biến các điểm M, N, P, Q theo thứ tự thành các điểm M’, N’, P’, Q’.

Ta thấy các đường thẳng MM’, NN’, PP’, QQ’ đồng quy tại I.

Xét phép vị tự tâm I, tỉ số k biến các điểm M, N, P, Q theo thứ tự thành các điểm M’, N’, P’, Q’.

Ta có \({V_{(I,{\rm{ }}k)}}\left( M \right){\rm{ }} = {\rm{ }}M’.\)

Suy ra và

Vì M, M’ nằm cùng phía đối với I nên \(k{\rm{ }} > {\rm{ }}0.\)

Do đó \(k = \frac{{OM’}}{{OM}}.\)

Tương tự ta cũng có \(k = \frac{{ON’}}{{ON}},k = \frac{{OP’}}{{OP}},k = \frac{{OQ’}}{{OQ}}\)

Do đó \(k = \frac{{OM’}}{{OM}} = \frac{{ON’}}{{ON}} = \frac{{OP’}}{{OP}} = \frac{{OQ’}}{{OQ}}\)

Vì vậy \({V_{\left( {I;\frac{{OM’}}{{OM}}} \right)}}\) là phép biến hình biến hình (A) thành hình (B).

⦁ Ta thấy OP’ = OP” và \(\widehat {P’OP”} = {90^o}\)

Suy ra phép quay tâm O, góc quay 90° biến điểm P’ thành điểm P”.

Chứng minh tương tự, ta thấy \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\;\) cũng biến các điểm khác trên hình (B) thành các điểm có vị trí tương ứng trên hình (C).

Vì vậy \({Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\;\) biến hình (B) thành hình (C).

⦁ Xét hai điểm N, P, ta có:

+) \(N’ = {\rm{ }}{V_{\left( {I,{\rm{ }}k} \right)}}\left( N \right){\rm{, }}N”{\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {N’} \right);\)

+) \(P'{\rm{ }} = {\rm{ }}{V_{\left( {I,{\rm{ }}k} \right)}}\left( P \right),P”{\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {P’} \right).\)

Do đó:

+) \(N’P'{\rm{ }} = {\rm{ }}{V_{(I,{\rm{ }}k)}}\left( {NP} \right)\). Suy ra \(N’P'{\rm{ }} = {\rm{ }}k.NP;\)

+) \(N”P”{\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {N’P’} \right).\)Suy ra \(N”P”{\rm{ }} = {\rm{ }}N’P’.\)

Vì vậy \(N”P” = {\rm{ }}N’P'{\rm{ }} = {\rm{ }}k.NP.\)

Vậy f là phép đồng dạng tỉ số k \(\left( {k{\rm{ }} > {\rm{ }}0} \right)\) biến (A) thành (C) thỏa mãn \(\left( B \right){\rm{ }} = {\rm{ }}{V_{\left( {I,{\rm{ }}k} \right)}}\left( {\left( A \right)} \right)\) và \(\left( C \right){\rm{ }} = {\rm{ }}{Q_{\left( {O,{\rm{ }}90^\circ } \right)}}\left( {\left( B \right)} \right);\)