Giải chi tiết Thực hành 2 Bài 2. Đường đi Euler và đường đi Hamilton (trang 50, 51, 52, 53, 54) – Chuyên đề học tập Toán 11 Chân trời sáng tạo. Hướng dẫn: Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả.
Câu hỏi/Đề bài:
Đồ thị sau có đường đi Euler không? Nếu có, hãy chỉ ra một đường đi như vậy.
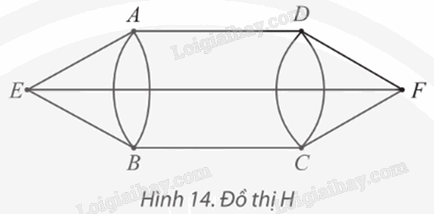
Hướng dẫn:
Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần.
Nếu chu trình là đường đi Euler thì chu trình đo được gọi là chu trình Euler.
Lời giải:
Ta có d(A) = d(B) = d(C) = d(D) = 4 và d(E) = d(F) = 3.
Suy ra đồ thị H có đúng 2 đỉnh bậc lẻ là E, F.
Do đó đồ thị H có đường đi Euler.
Chẳng hạn, bắt đầu từ đỉnh E, ta có thể đi theo đường đi Euler: EAabADcdDFCBEF.