Hướng dẫn giải Thực hành 1 Bài 3. Phép đối xứng trục (trang 15, 16, 17) – Chuyên đề học tập Toán 11 Chân trời sáng tạo. Hướng dẫn: Nếu \(M’ = {Đ_{Ox}}(M)\) thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M’}} = {x_M}\\{y_{M’}} = – {y_M}\end{array} \right. \.
Câu hỏi/Đề bài:
Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(d:{\rm{ }}x-y + 3 = 0\) và đường tròn \(\left( C \right):{\rm{ }}{\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2}\; = 9.\)
a) Tìm ảnh của đường thẳng d qua \({Đ_{Oy}}.\)
b) Tìm ảnh của đường tròn (C) qua \({Đ_{Ox}}.\)
Hướng dẫn:
Nếu \(M’ = {Đ_{Ox}}(M)\) thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M’}} = {x_M}\\{y_{M’}} = – {y_M}\end{array} \right.\)
Nếu \(M’ = {Đ_{Oy}}(M)\) thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M’}} = – {x_M}\\{y_{M’}} = {y_M}\end{array} \right.\)
Lời giải:
a) Trục \(Oy:{\rm{ }}x = 0.\)
Thế x = 0 vào phương trình d, ta được \(0{\rm{ }}-{\rm{ }}y{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}0 \Leftrightarrow y{\rm{ }} = {\rm{ }}3.\)
Suy ra giao điểm của d và Oy là \(P\left( {0;{\rm{ }}3} \right).\)
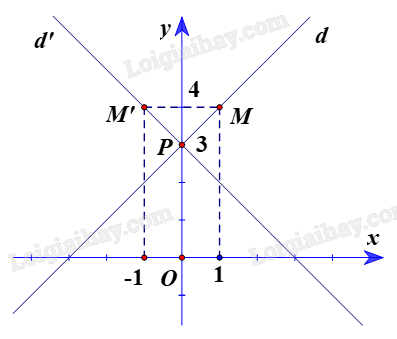
Chọn điểm \(M\left( {1;{\rm{ }}4} \right) \in d:{\rm{ }}x{\rm{ }}-{\rm{ }}y{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}0\)
Ta đặt \(M'{\rm{ }} = {\rm{ }}{Đ_{Oy}}\left( M \right).\)
Suy ra Oy là đường trung trực của MM’ hay M’ là điểm đối xứng với M qua Oy.
Do đó hai điểm M và M’ có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ điểm M’(-1; 4).
Ta có \(\overrightarrow {M’P} = \left( {1; – 1} \right)\)
Gọi d’ là ảnh của d qua \({Đ_{Oy}}.\)
Đường thẳng d’ có vectơ chỉ phương \(\overrightarrow {M’P} = \left( {1; – 1} \right)\).
Suy ra d’ có vectơ pháp tuyến \({\vec n_{d’}} = \left( {1;1} \right)\)
Vậy đường thẳng d’ đi qua P(0; 3) và có vectơ pháp tuyến \({\vec n_{d’}} = \left( {1;1} \right)\) nên phương trình d’ là: \(1.\left( {x{\rm{ }}-{\rm{ }}0} \right){\rm{ }} + {\rm{ }}1.\left( {y{\rm{ }}-{\rm{ }}3} \right){\rm{ }} = {\rm{ }}0\; \Leftrightarrow x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}3{\rm{ }} = {\rm{ }}0.\)
b) Đường tròn (C) có tâm I(-1; -2), bán kính R = 3.
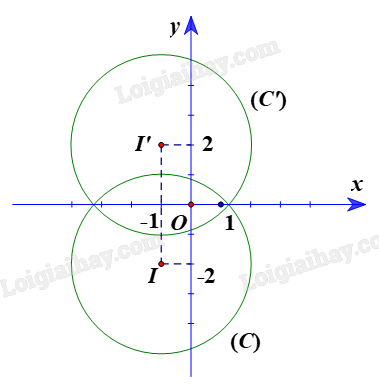
Ta đặt \(I'{\rm{ }} = {\rm{ }}{Đ_{Ox}}\left( I \right).\)
Suy ra Ox là đường trung trực của II’ hay I’ đối xứng với I qua Ox
Do đó hai điểm I và I’ có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ điểm I’(-1; 2).
Gọi (C’) là ảnh của đường tròn (C) qua ĐOx.
Suy ra (C’) có tâm I’(-1; 2), bán kính \(R'{\rm{ }} = {\rm{ }}R{\rm{ }} = {\rm{ }}3.\)
Vậy phương trình đường tròn \(\left( {C’} \right):{\rm{ }}{\left( {x{\rm{ }} + {\rm{ }}1} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}2} \right)^2}\; = {\rm{ }}9.\)