Giải Khám phá 2 Bài 2. Đường đi Euler và đường đi Hamilton (trang 50, 51, 52, 53, 54) – Chuyên đề học tập Toán 11 Chân trời sáng tạo. Hướng dẫn: Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất.
Câu hỏi/Đề bài:
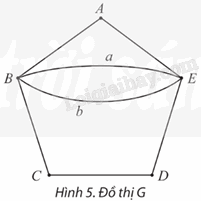
a) Chỉ ra một chu trình Euler của đồ thị G ở Hình 5. Đồ thị này có đỉnh nào bậc lẻ không?
b) Chỉ ra rằng các đồ thị S và T sau đây không có chu trình Euler. Các đồ thị này có đỉnh bậc lẻ không?

Hướng dẫn:
– Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần. Nếu chu trình là đường đi Euler thì chu trình đo được gọi là chu trình Euler.
– Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là \(d(A)\)
– Đỉnh có bậc là số chẵn gọi là đỉnh bậc chẵn, đỉnh có bậc là một số lẻ là đỉnh bậc lẻ.
Lời giải:
a) Một chu trình Euler của đồ thị G là: AB, a, b, BC, CD, DE, EA.
Ta có d(A) = 2; d(B) = 4; d(C) = 2; d(D) = 2; d(E) = 4.
Vậy đồ thị đã cho không có đỉnh nào là đỉnh bậc lẻ.
b) Đồ thị S không có chu trình Euler vì nếu một đường đi bắt đầu và kết thúc tại cùng một đỉnh thì cạnh CD bắt buộc phải đi qua ít nhất hai lần; nếu một đường đi bắt đầu tại đỉnh này và kết thúc tại đỉnh kia thì không được gọi là chu trình.
Tương tự như vậy, đồ thị T không có chu trình Euler.
Đồ thị S có: d(A) = 2; d(B) = 2; d(C) = 3; d(D) = 1.Suy ra đồ thị S có hai đỉnh bậc lẻ là C, D.
Đồ thị T có: d(A) = 3; d(B) = 2; d(C) = 3; d(D) = 2.Suy ra đồ thị T có hai đỉnh bậc lẻ là A, C.
Vậy cả hai đồ thị S và T đều có đỉnh bậc lẻ.