Hướng dẫn giải Khám phá 1 Bài 6. Phép vị tự (trang 30, 31, 32) – Chuyên đề học tập Toán 11 Chân trời sáng tạo. Gợi ý: Quan sát hình 1 và chứng minh 2 tam giác đồng dạng theo trường hợp c. c.
Câu hỏi/Đề bài:
Trong Hình 1, cho biết A’, B’, C’ lần lượt là trung điểm của OA, OB, OC.
a) Xét xem hai tam giác ABC và A’B’C’ đồng dạng không?
b) Thảo luận nhóm để tìm xem có phép biến hình nào biến tam giác ABC thành tam giác A’B’C’ không?
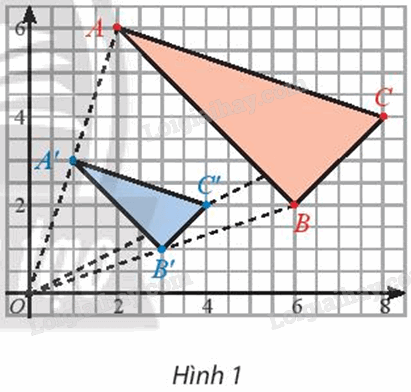
Hướng dẫn:
Quan sát hình 1 và chứng minh 2 tam giác đồng dạng theo trường hợp c.c.c
Lời giải:
a) Ta có A’ là trung điểm của OA.
Suy ra \(OA’ = \frac{1}{2}OA\) hay \(\frac{{OA’}}{{OA}} = \frac{1}{2}\)
Chứng minh tương tự, ta được \(\frac{{OB’}}{{OB}} = \frac{1}{2}\) và \(\frac{{OC’}}{{OC}} = \frac{1}{2}\)
Do \(\frac{{OA’}}{{OA}} = \frac{{OB’}}{{OB}}\left( { = \frac{1}{2}} \right)\) nên áp dụng định lí Thales đảo, ta được A’B’ // AB.
Từ A’B’ // AB, theo hệ quả định lí Thales ta có: \(\frac{{A’B’}}{{AB}} = \frac{{OA’}}{{OA}} = \frac{1}{2}\) hay \(\frac{{AB}}{{A’B’}} = 2\)
Chứng minh tương tự, ta được \(\frac{{BC}}{{B’C’}} = 2\) và \(\frac{{AC}}{{A’C’}} = 2\)
Xét \(\Delta ABC{\rm{ }}\) và có:
\(\frac{{AB}}{{A’B’}} = \frac{{BC}}{{B’C’}} = \frac{{AC}}{{A’C’}}\left( { = 2} \right)\)
Vậy \(\Delta ABC\) đồng dạng với \(\Delta A\prime B\prime C\prime \) (c.c.c).
b) Để tìm phép biến hình biến ∆ABC thành ∆A’B’C’, ta tìm phép biến hình biến điểm A thành điểm A’, biến điểm B thành điểm B’, biến điểm C thành điểm C’.
Ta có A’ là trung điểm OA (giả thiết).
Suy ra \(\overrightarrow {OA’} = \frac{1}{2}\overrightarrow {OA} \)
Do đó phép biến hình biến điểm A thành điểm A’ thỏa mãn \(\overrightarrow {OA’} = \frac{1}{2}\overrightarrow {OA} \,\,(1)\)
Thực hiện tương tự, ta được \(\overrightarrow {OB’} = \frac{1}{2}\overrightarrow {OB} \)
Suy ra phép biến hình biến điểm B thành điểm B’ thỏa mãn \(\overrightarrow {OB’} = \frac{1}{2}\overrightarrow {OB} \,\,(2)\)
Thực hiện tương tự, ta được \(\overrightarrow {OC’} = \frac{1}{2}\overrightarrow {OC} \)
Do đó phép biến hình biến điểm C thành điểm C’ sao cho \(\overrightarrow {OC’} = \frac{1}{2}\overrightarrow {OC} \,\,(3)\)
Từ (1), (2), (3), ta thu được phép biến hình biến \(\Delta ABC\) thành là phép biến hình biến ba điểm A, B, C thành ba điểm A’, B’, C’ thỏa mãn \(\overrightarrow {OA’} = \frac{1}{2}\overrightarrow {OA} ,\,\overrightarrow {OB’} = \frac{1}{2}\overrightarrow {OB} ,\,\overrightarrow {OC’} = \frac{1}{2}\overrightarrow {OC} \) với O là giao điểm của ba đường thẳng AA’, BB’, CC’.