Quan sát hình vẽ và sử dụng hệ quả: Phép vị tự tỉ số k biến đoạn thẳng thành đoạn thẳng nhân lên với |k|. Vận dụng kiến thức giải Giải bài 7 trang 36 Chuyên đề học tập Toán 11 Chân trời sáng tạo – Bài 6. Phép vị tự – Chuyên đề học tập Toán 11 Chân trời sáng tạo. Tìm các tỉ số vị tự của phép biến hình được thực hiện trên cây thước vẽ truyền trong Hình…
Đề bài/câu hỏi:
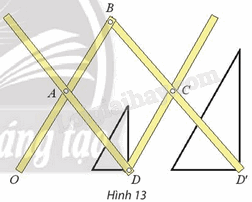
Tìm các tỉ số vị tự của phép biến hình được thực hiện trên cây thước vẽ truyền trong Hình 13.
Hướng dẫn:
Quan sát hình vẽ và sử dụng hệ quả:
Phép vị tự tỉ số k biến đoạn thẳng thành đoạn thẳng nhân lên với |k|, biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng |k|, biến đường tròn bán kính r thành đường tròn bán kính \(r’ = |k|.r\).
Lời giải:
Xét hình tam giác đỉnh D khi vẽ truyền cho ta hình tam giác đỉnh D’ là ảnh của hình D.
Ta có ba điểm O, D, D’ thẳng hàng nên \(\overrightarrow {OD’} = k\overrightarrow {OD} \).
Do đó \(\;{V_{(O,{\rm{ }}k)}}\left( D \right){\rm{ }} = {\rm{ }}D’\) và \(OD'{\rm{ }} = {\rm{ }}\left| k \right|.OD.\)
Vì D, D’ nằm cùng phía đối với O nên \(k{\rm{ }} > {\rm{ }}0.\)
Suy ra \(k = \frac{{OD’}}{{OD}}\)
Ta có AB // BD’ (do ABCD là hình bình hành) và ba điểm O, D, D’ thẳng hàng (giả thiết).
Khi đó áp dụng định lí Thales, ta được \(k = \frac{{OD}}{{OD’}} = \frac{{OA}}{{OB}}\)
Vậy phép vị tự biến hình tam giác có đỉnh D thành tam giác có đỉnh D’ là \({V_{\left( {O,\frac{{OA}}{{OB}}} \right)}}\)
Ngược lại, phép vị tự biến hình tam giác đỉnh D’ khi vẽ truyền cho ta hình tam giác đỉnh D là ảnh của hình D là \({V_{\left( {O,\frac{{OB}}{{OA}}} \right)}}\)