Giải chi tiết Luyện tập 2 Bài 2. Một vài ứng dụng của lí thuyết đồ thị (trang 44, 45, 46) – Chuyên đề học tập Toán 11 Cánh diều. Gợi ý: Để tìm quãng đường đi ngắn nhất trên đồ thị có trọng số.
Câu hỏi/Đề bài:
Sử dụng thuật toán láng giềng gần nhất để giải bài toán trong Hoạt động 2.
Hướng dẫn:
Để tìm quãng đường đi ngắn nhất trên đồ thị có trọng số, ta áp dụng thuật toán láng giềng gần nhất để tìm tất cả các chu trình xuất phát từ một đỉnh ban đầu, đi qua các đỉnh khác và trở về đỉnh ban đầu sao cho tổng độ dài các cạnh của chu trình đó là ngắn nhất. Sau đó, ta so sánh độ dài của tất cả các chu trình “tốt nhất” vừa tìm được để tìm ra chu trình có tổng độ dài các cạnh là ngắn nhất.
Lời giải:
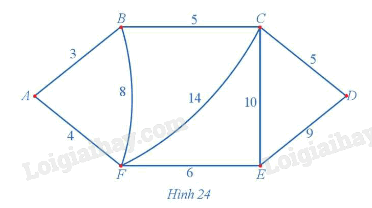
Dễ thấy đồ thị Hình 24 có chu trình Hamilton.
+) Sử dụng thuật toán láng giềng gần nhất đối với đỉnh xuất phát A, ta có:
Từ A, đỉnh gần nhất là B, AB = 3 km;
Từ B, đỉnh chưa đến gần nhất là C, BC = 5 km;
Từ C, đỉnh chưa đến gần nhất là D, CD = 5 km;
Từ D, đỉnh chưa đến gần nhất là E, DE = 9 km;
Từ E, đỉnh chưa đến gần nhất là F, EF = 6 km;
Đến đây không còn đỉnh chưa đến, vì vậy quay về A, FA = 4 km.
Tổng quãng đường theo chu trình ABCDEFA là: 3 + 5 + 5 + 9 + 6 + 4 = 32 (km).
Tương tự bắt đầu với những đỉnh khác, ta có bảng sau:
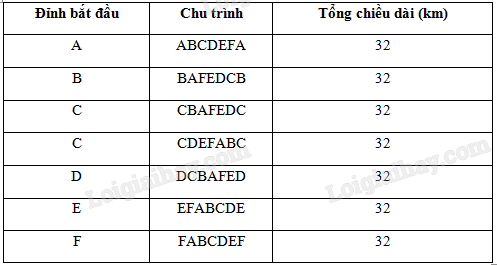
Vậy người giao hàng chọn 1 đường đi trong 7 đường đi trên thì quãng đường phải di chuyển là ngắn nhất.