Giải chi tiết Luyện tập 10 Bài 1. Một vài yếu tố của Lí thuyết đồ thị. Đường đi Euler và đường đi Hamilton (trang 40, 41, 42, 43) – Chuyên đề học tập Toán 11 Cánh diều. Gợi ý: Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả.
Câu hỏi/Đề bài:
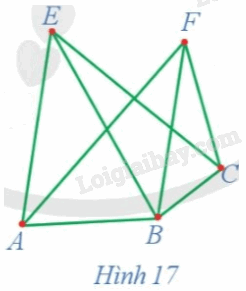
Chứng minh rằng đồ thị G ở Hình 17 có ít nhất một chu trình Hamilton.
Hướng dẫn:
Trong đồ thị, một đường đi được gọi là đường đi Hamilton nếu đường đi đó đi qua tất cả các đinht của đồ thị, mỗi đỉnh đúng 1 lần.
Nếu chu trình là đường đi Hamilton thì chu trình đó được gọi là chu trình Hamilton
Lời giải:
Ta có: d(A) = 3, d(B) = 4, d(C) = 3, d(E) = 3, d(F) = 3. Đồ thị G ở Hình 17 gồm 5 đỉnh, mỗi đỉnh của đồ thị đều có bậc không nhỏ hơn \(\frac{5}{2}\) . Do đó, theo định lí Dirac, đồ thị G có ít nhất một chu trình Hamilton.