Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’. Giải chi tiết Giải bài 7 trang 33 Chuyên đề học tập Toán 11 Cánh diều – Bài 2. Phép đồng dạng – Chuyên đề học tập Toán 11 Cánh diều. Cho tam giác nhọn ABC có trực tâm H….
Đề bài/câu hỏi:
Cho tam giác nhọn ABC có trực tâm H. Xác định ảnh của tam giác ABC qua phép vị tự tâm H tỉ số \(k = \frac{1}{2}\).
Hướng dẫn:
– Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A’B’ = \left| k \right|AB\)
– Để xác định ảnh của tam giác ABC qua phép vị tự tâm H tỉ số \(k = \frac{1}{2}\), ta xác định ảnh của từng điểm A, B, C qua phép vị tự tâm H tỉ số \(k = \frac{1}{2}\).
Lời giải:
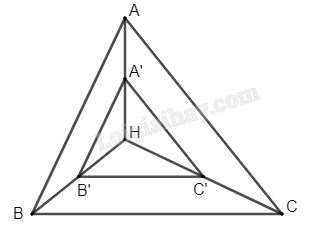
Gọi A’, B’, C’ lần lượt là ảnh của A, B, C qua phép vị tự tâm H tỉ số \(k = \frac{1}{2}\).
Khi đó ta có: \(\overrightarrow {HA’} = \frac{1}{2}\overrightarrow {HA} ;\,\,\overrightarrow {HB’} = \frac{1}{2}\overrightarrow {HB} ;\,\,\overrightarrow {HC’} = \frac{1}{2}\overrightarrow {HC} \)
Từ đó suy ra A’, B’, C’ lần lượt là trung điểm của AH, BH, CH.
Vậy ảnh của tam giác ABC qua phép vị tự tâm H tỉ số \(k = \frac{1}{2}\) là tam giác A’B’C’ với A’, B’, C’ lần lượt là trung điểm của AH, BH, CH.