Bước 1. Chọn một đỉnh bắt đầu, ta gọi là đỉnh V. Bước 2. Xuất phát từ đỉnh hiện hành. Hướng dẫn cách giải/trả lời Giải bài 4 trang 49 Chuyên đề học tập Toán 11 Cánh diều – Bài 2. Một vài ứng dụng của lí thuyết đồ thị – Chuyên đề học tập Toán 11 Cánh diều. Sử dụng thuật toán láng giềng gần nhất,…
Đề bài/câu hỏi:
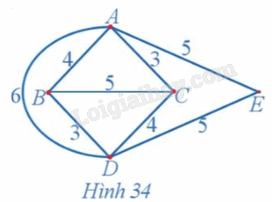
Sử dụng thuật toán láng giềng gần nhất, hãy giải bài toán người giao hàng đối với đồ thị ở Hình 34, số ghi trên mỗi cạnh của đồ thị mô tả độ dài quãng đường giữa các địa điểm (đơn vị: kilômét).
Hướng dẫn:
Bước 1. Chọn một đỉnh bắt đầu, ta gọi là đỉnh V.
Bước 2. Xuất phát từ đỉnh hiện hành, chọn cạnh có độ dài nhỏ nhất nối đến một trong các đỉnh chưa đến. Đánh dấu đỉnh cuối của cạnh vừa chọn.
Bước 3. Xuất phát từ đỉnh vừa đánh dấu, nếu còn đỉnh chưa đến thì quay lại bước 2.
Bước 4. Quay lại đỉnh V.
Lời giải:
Dễ thấy đồ thị Hình 34 có chu trình Hamilton.
Ta thấy chu trình xuất phát từ đỉnh A là AEDBCA thỏa mãn đề bài với tổng quãng đường nhỏ nhất là AE + ED + DB + BC + CA = 5 + 5 + 3 + 5 + 3 = 21 (km).
Các chu trình xuất phát từ đỉnh B, C, D, E có 1 đỉnh được đi qua hai lần nên không thỏa mãn quy tắc của thuật toán láng giềng gần nhất nên loại.