Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là \(d(A)\. Trả lời Giải bài 3 trang 43 Chuyên đề học tập Toán 11 Cánh diều – Bài 1. Một vài yếu tố của Lí thuyết đồ thị. Đường đi Euler và đường đi Hamilton – Chuyên đề học tập Toán 11 Cánh diều. Tìm bậc của mỗi đỉnh và chỉ ra một chu trình Euler (nếu có) của đồ thị ở Hình 20….
Đề bài/câu hỏi:
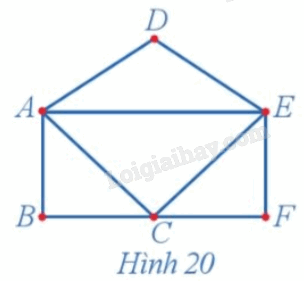
Tìm bậc của mỗi đỉnh và chỉ ra một chu trình Euler (nếu có) của đồ thị ở Hình 20.
Hướng dẫn:
Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là \(d(A)\)
Trong đồ thị, một đường đi được gọi là đường đi Euler nếu đường đi đó đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần. Nếu chu trình là đường đi Euler thì chu trình đo được gọi là chu trình Euler.
Lời giải:
Ta có: d(A) = 4, d(B) = 2, d(C) = 4, d(D) = 2, d(E) = 4, d(F) = 2.
Vì đồ thị Hình 20 liên thông và không có đỉnh bậc lẻ nên theo định lí Euler thì đồ thị này có chu trình Euler.
Một chu trình Euler của đồ thị ở Hình 20 là AECFEDACBA.