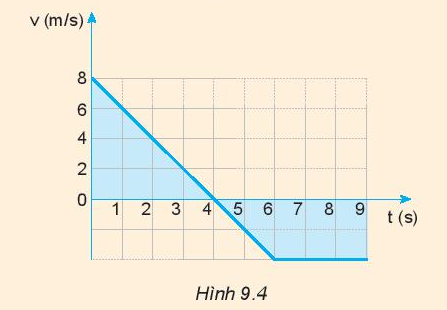
Câu 3 trang 42 Vật Lí 10 – Kết nối tri thức: Hãy dùng đồ thị (v – t) vẽ ở hình 9.4 để: a) Mô tả chuyển động b) Tính độ dịch chuyển trong 4 giây đầu

Câu hỏi/Đề bài:

Hướng dẫn:

– Dựa vào đồ thị hình 9.4 để mô tả chuyển động.

– Sử dụng công thức tính độ dịch chuyển, gia tốc.

Lời giải:

a) Mô tả chuyển động:

– Trong 4 giây đầu tiên: chuyển động chậm dần đều từ 8 m/s đến 0 m/s

– Từ giây thứ 4 đến giây thứ 6: bắt đầu tăng tốc với vận tốc -2 m/s

– Từ giây thứ 6 đến giây thứ 9: chuyển động thẳng đều với vận tốc – 2 m/s

b) Độ dịch chuyển:

– Trong 4 giây đầu:

Độ dịch chuyển bằng diện tích tam giác vuông có cạnh đáy là t và chiều cao là v.

\({d_1} = \frac{1}{2}.{t_1}.{v_1} = \frac{1}{2}.4.8 = 16\left( m \right)\)

– Trong 2 giây tiếp theo:

Độ dịch chuyển bằng diện tích tam giác vuông có cạnh đáy là t và chiều cao là v.

\({d_2} = \frac{1}{2}.{t_2}.{v_2} = \frac{1}{2}.2.( – 4) = – 4\left( m \right)\)

– Trong 3 giây cuối:

Độ dịch cuyển bằng diện tích hình chữ nhật có chiều dài là t và chiều rộng là v.

\({d_3} = {v_3}.{t_3} = – 4.3 = – 12\left( m \right)\)

c)

Gia tốc của chuyển động trong 4 giây đầu:

\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{0 – 8}}{{4 – 0}} = – 2\left( {m/{s^2}} \right)\)

d)

Gia tốc của chuyển động từ giây thứ 4 đến giây thứ 6:

\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{ – 4 – 0}}{{6 – 4}} = – 2\left( {m/{s^2}} \right)\)

* Kiểm tra kết quả bằng công thức:

Độ dịch chuyển:

– Trong 4 giây đầu:

\({d_1} = {v_0}.{t_1} + \frac{1}{2}.a.t_1^2 = 8.4 + \frac{1}{2}.( – 2){.4^2} = 16(m)\)

– Trong 2 giây tiếp theo:

\({d_2} = {v_0}{t_2} + \frac{1}{2}a{t_2}^2 = 0.2 + \frac{1}{2}.( – 2){.2^2} = – 4\left( m \right)\)

– Trong 3 giây cuối:

\({d_3} = {v_3}t = – 4.3 = – 12\left( m \right)\)

=> Trùng với kết quả khi dùng đồ thị.