Đáp án Câu hỏi trang 44 Luyện tập Bài 7. Gia tốc – Chuyển động thẳng biến đổi đều SGK Vật Lí 10 Chân trời sáng tạo. Hướng dẫn: Biểu thức tính gia tốc: \(a = \frac{{{v_2} – {v_1}}}{{{t_2} – {t_1}}}\.
Câu hỏi/Đề bài:
|
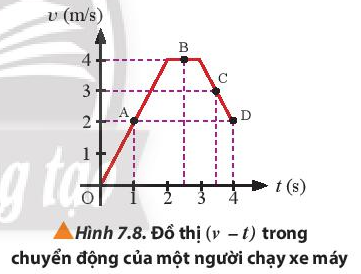
Một người chạy xe máy theo một đường thẳng và có vận tốc theo thời gian được biểu diễn bởi đồ thị (v – t) như Hình 7.8. Xác định: a) Gia tốc của người này tại các thời điểm 1 s, 2,5 s và 3,5 s. b) Độ dịch chuyển của người này từ khi bắt đầu chạy đến thời điểm 4 s.
|
Hướng dẫn:
Biểu thức tính gia tốc: \(a = \frac{{{v_2} – {v_1}}}{{{t_2} – {t_1}}}\)
Độ dịch chuyển của vật trong khoảng thời gian từ t1 đến t2 được xác định bằng phần diện tích giới hạn bởi các đường v(t), v = 0, t = t1, t = t2 trong đồ thị (v – t).
Lời giải chi tiết:
a) Gia tốc của người này tại các thời điểm là:
+ t = 1 s: \(a = \frac{{{v_2} – {v_1}}}{{{t_2} – {t_1}}} = \frac{2}{1} = 2(m/{s^2})\)
+ t = 2,5 s: \(a = 0 (m/{s^2})\)
+ t = 3,5 s: \(a = \frac{{{v_2} – {v_1}}}{{{t_2} – {t_1}}} = \frac{3-4}{{3,5-3}}=-2(m/{s^2})\)
b)
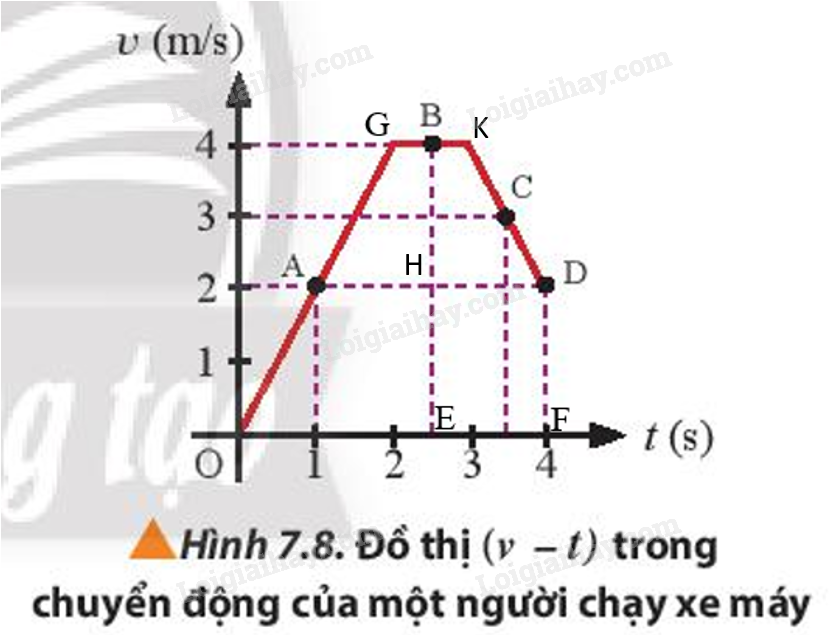
Độ dịch chuyển = Diện tích hình thang OGBE + Diện tích hình thang BKDH + Diện tích hình chữ nhật HDFE
=> Độ dịch chuyển của người này là:
\(\begin{array}{l}d = \frac{1}{2}.(BG + OE).BE + \frac{1}{2}.(BK + HD).BH\ + (EF.DF)\ = \frac{1}{2}.(0,5 + 2,5).4 + \frac{1}{2}.(0,5 + 1,5).2 + 2.1,5 = 11(m)\end{array}\)