Bước 1: Gọi x là độ dài AM. Biểu diễn độ dài BM và MD theo x Bước 2. Lời giải bài tập, câu hỏi Giải bài 6.61 trang 27 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài tập cuối Chương 6. Cho hình chữ nhật ABCD có AB = 6 cm, AD = 13 cm….
Đề bài/câu hỏi:
Cho hình chữ nhật ABCD có AB = 6 cm, AD = 13 cm. Tìm vị trí điểm M trên cạnh AD sao cho BM = 2MD
Hướng dẫn:
Bước 1: Gọi x là độ dài AM. Biểu diễn độ dài BM và MD theo x
Bước 2: Lập phương trình ẩn x theo giả thiết BM = 2MD
Bước 3: Giải phương trình vừa tìm được ở bước 2 rồi kết luận
Lời giải:
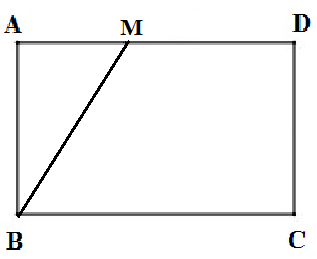
Gọi x (cm) (0 < x < 13) là độ dài AM.
Khi đó MD = 13 – x (cm) và BM = \(\sqrt {A{M^2} + A{B^2}} = \sqrt {{x^2} + 36} \) (cm)
Theo giả thiết, BM = 2MD \( \Leftrightarrow \sqrt {{x^2} + 36} = 2(13 – x)\) (*)
Bình phương 2 vế PT (*) ta có:
\({x^2} + 36 = 4{x^2} – 104x + 676 \Leftrightarrow 3{x^2} – 104x + 640 = 0 \Leftrightarrow x = \frac{{80}}{3}\) hoặc x = 8
Kết hợp với điều kiện, PT (*) có nghiệm duy nhất x = 8
Vậy với AM = 8 cm thì BM = 2MD.