Chứng minh tứ giác \(ABHC\) là hình bình hành – Chứng minh \(M\) là trung điểm của \(A’H\) – Chứng minh \(MO\. Phân tích, đưa ra lời giải Giải bài 4.5 trang 47 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài 7. Các khái niệm mở đầu. Cho tam giác ABC không vuông, với trực tâm H, nội tiếp đường tròn (O)….
Đề bài/câu hỏi:
Cho tam giác \(ABC\) không vuông, với trực tâm \(H\), nội tiếp đường tròn \((O).\) Kẻ đường kính \(AA’\) của đường tròn \((O).\)
a) Chứng minh rằng \(\overrightarrow {BH} = \overrightarrow {A’C} .\)
b) Gọi \(M\) là trung điểm của \(BC.\) Tìm mối quan hệ về phương, hướng và độ dài của hai vectơ \(\overrightarrow {AH} \) và \(\overrightarrow {OM} .\)
Hướng dẫn:
– Chứng minh tứ giác \(ABHC\) là hình bình hành
– Chứng minh \(M\) là trung điểm của \(A’H\)
– Chứng minh \(MO\) là đường trung bình của \(\Delta AA’H\)
Lời giải:
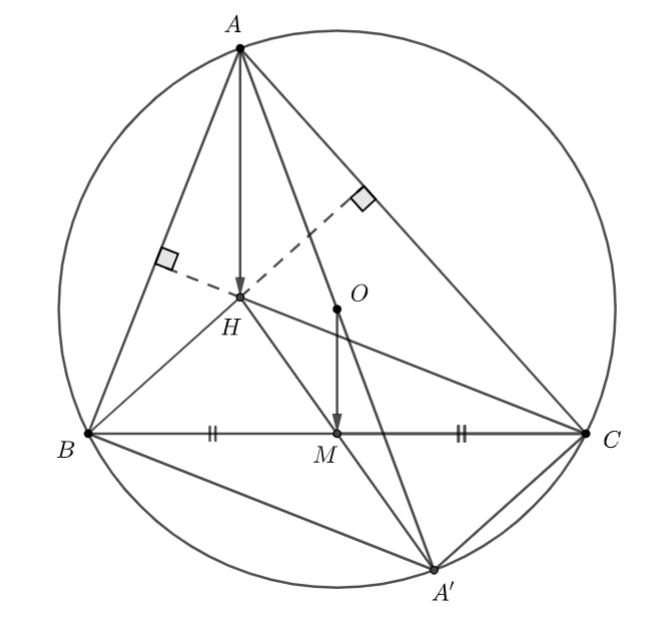
a) Xét \((O)\) có: \(\widehat {ABA’} = \widehat {ACA’} = {90^ \circ }\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow A’C \bot AC\) và \(A’B \bot AB\) (1)
Ta có: \(H\) là trực tâm của tam giác \(ABC.\)
\( \Rightarrow BH \bot AC\) và \(CH \bot AB\) (2)
Từ (1) và (2) \( \Rightarrow \) \(BH\)//\(A’C\) và \(A’B\)//\(CH.\)
Xét tứ giác \(ABHC\) có: \(BH\)//\(A’C\) và \(A’B\)//\(CH\)
\( \Rightarrow \) tứ giác \(ABHC\) là hình bình hành (dấu hiệu nhận biết)
\( \Rightarrow \overrightarrow {BH} = \overrightarrow {A’C} \)
b) Ta có: tứ giác \(ABHC\) là hình bình hành
nên \(M\) là trung điểm của \(A’H\)
Xét \(\Delta AA’H\) có: \(M\) là trung điểm của \(A’H\)
\(O\) là trung điểm của \(AA’\)
\( \Rightarrow \) \(MO\) là đường trung bình của \(\Delta AA’H\)
\( \Rightarrow \) \(MO\)//\(AH\) và \(2MO = AH\)
\( \Rightarrow \) hai vectơ \(\overrightarrow {MO} ,\,\,\overrightarrow {AH} \) cùng hướng và \(2\overrightarrow {OM} = \overrightarrow {AH} .\)