Chứng minh tứ giác \(ABEC\) là hình chữ nhật – Áp dụng Py-ta-go để tính cạnh \(AE\): \(A{E^2} = A{B^2} + A{C^2}\. Hướng dẫn cách giải/trả lời Giải bài 4.11 trang 51 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài 8. Tổng và hiệu của hai vectơ. Trên Hình 4.7 biểu diễn ba lực…
Đề bài/câu hỏi:
Trên Hình 4.7 biểu diễn ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) cùng tác động vào một vị trí cân bằng \(A.\) Cho biết \(\left| {\overrightarrow {{F_1}} } \right| = 30N,\,\,\left| {\overrightarrow {{F_2}} } \right| = 40N.\) Tính cường độ của lực \(\overrightarrow {{F_3}} .\)
Hướng dẫn:
– Chứng minh tứ giác \(ABEC\) là hình chữ nhật
– Áp dụng Py-ta-go để tính cạnh \(AE\): \(A{E^2} = A{B^2} + A{C^2}\)
– Do vật ở vị trí cân bằng nên \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow F } \right| = AE\)
Lời giải:
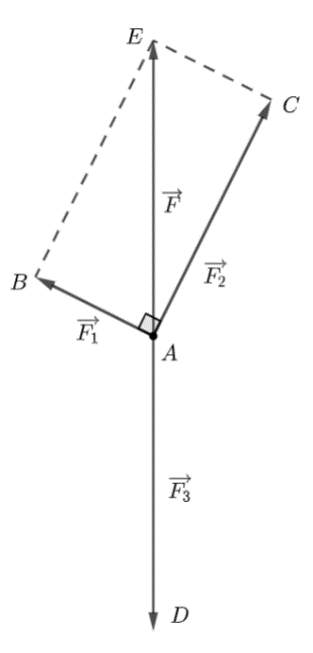
Ta có: \(\widehat {BAC} = {90^ \circ }\)
Nên tứ giác \(ABEC\) là hình chữ nhật
\( \Rightarrow \) \(\left| {\overrightarrow F } \right| = AE = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{30}^2} + {{40}^2}} = 50\,\,(N)\)
Do vật ở vị trí cân bằng nên hai lực \(\overrightarrow F \) và \(\overrightarrow {{F_3}} \) có cùng cường độ và ngược chiều nhau
\( \Rightarrow \) \(\left| {\overrightarrow {F{}_3} } \right| = \left| {\overrightarrow F } \right| = AD = 50\,\,(N)\)