Gọi đường thẳng \(d\) cần tìm là: \(d: y = ax + b, \, \, \left( {a \ne 0} \right). \. Hướng dẫn giải Giải bài 2.3 trang 18 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài 3. Bất phương trình bậc nhất hai ẩn. Xác định một bất phương trình bậc nhất hai ẩn nhân nửa mặt phẳng bờ là đường thẳng d (miền…
Đề bài/câu hỏi:
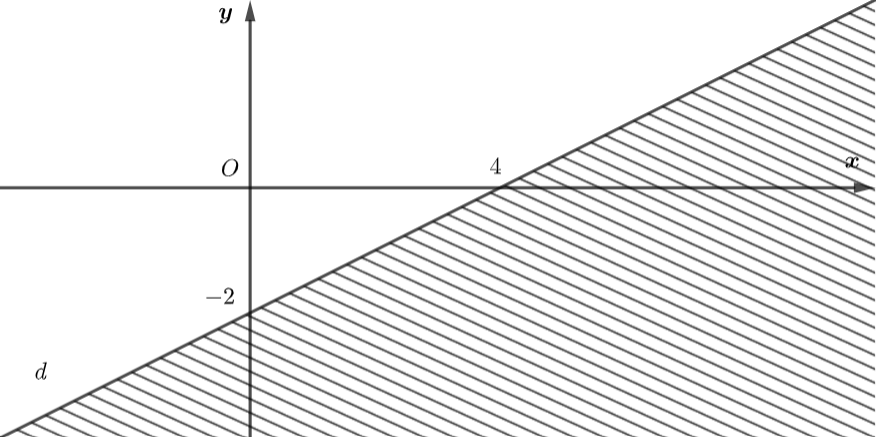
Xác định một bất phương trình bậc nhất hai ẩn nhân nửa mặt phẳng bờ là đường thẳng \(d\) (miền không bị gạch) làm miền nghiệm.
Hướng dẫn:
– Gọi đường thẳng \(d\) cần tìm là: \(d:y = ax + b,\,\,\left( {a \ne 0} \right).\)
– Xác định đường thẳng \(d\)
– Từ miền nghiệm của bất phương trình, kết luận bất phương trình cần tìm.
Lời giải:
Gọi đường thẳng \(d\) cần tìm là: \(d:y = ax + b,\,\,\left( {a \ne 0} \right).\)
Nhìn vào độ thị thì đường thẳng \(d\) đi qua điểm \(A\left( {4;0} \right)\) và \(B\left( {0; – 2} \right)\)
Thay điểm \(A\left( {4;0} \right)\) vào \(d\) ta được: \(4a + b = 0.\)
Thay điểm \(B\left( {0; – 2} \right)\) vào \(d\) ta được: \(0a + b = – 2\,\, \Rightarrow \,\,b = – 2\)
Ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{c}}{4a + b = 0}\\{b = – 2}\end{array}} \right.\,\, \Rightarrow \,\,\left\{ {\begin{array}{*{20}{c}}{a = \frac{1}{2}}\\{b = – 2}\end{array}} \right.\)
\( \Rightarrow \,\,d:y = \frac{1}{2}x – 2\,\, \Leftrightarrow \,\,x – 2y = 4.\)
Vì miền nghiệm của đồ thị là nửa mặt phẳng bờ \(d\) chứa điểm \(O\) nên bất phương trình cần tìm là: \(x – 2y \le 4\)