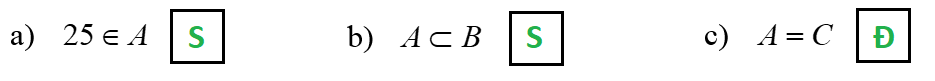Giải phương trình \({x^3} – 52{x^2} + 667x = 0. \) Liệt kê các phần tử thỏa mãn các tập hợp đã cho. Gợi ý giải Giải bài 1.39 trang 15 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài tập cuối Chương 1. Hãy điền Đ vào ô trống nếu mệnh đề đúng, điền S vào ô trống nếu mệnh đề sai….
Đề bài/câu hỏi:
Cho các tập hợp sau:
A ={x là số nguyên tố và \(20 \le x \le 30\)}
B ={x là bội của 18 và \(20 \le x \le 30\)}
C là tập hợp các nghiệm dương của phương trình \({x^3} – 52{x^2} + 667x = 0.\)
Hãy điền Đ vào ô trống nếu mệnh đề đúng, điền S vào ô trống nếu mệnh đề sai.
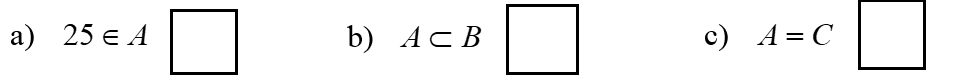
Hướng dẫn:
– Giải phương trình \({x^3} – 52{x^2} + 667x = 0.\)
– Liệt kê các phần tử thỏa mãn các tập hợp đã cho.
– Điền Đ hoặc S vào ô trống.
Lời giải:
Giải phương trình \({x^3} – 52{x^2} + 667x = 0\,\, \Leftrightarrow \,\,\left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 23}\\{x = 29}\end{array}.} \right.\)
Vì phương trình lấy nghiệm dương nên \(x = 23\) và \(x = 29\) thỏa mãn.
\(A = \left\{ {23;29} \right\};\quad B = \emptyset ;\quad C = \left\{ {23;29} \right\}.\)