\(A \cap B= \{ x \in A| x \in B\};\\ A\backslash B = \{ x \in A| x \notin B\}. Phân tích, đưa ra lời giải Giải bài 1.37 trang 15 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài tập cuối Chương 1. Viết hai tập hợp trên dưới dạng khoảng, đoạn….
Đề bài/câu hỏi:
Cho hai tập hợp sau:
\(A = \left\{ {\left. {x \in \mathbb{R}} \right|\left| x \right| \le 4} \right\};\quad B = \left\{ {\left. {x \in \mathbb{R}} \right| – 3 < x \le 8} \right\}\)
a) Viết hai tập hợp trên dưới dạng khoảng, đoạn.
b) Xác định các tập hợp sau: \(A \cap B;\,\,A\backslash B;\,\,B\backslash A\).
Hướng dẫn:
\(A \cap B= \{ x \in A| x \in B\};\\ A\backslash B = \{ x \in A| x \notin B\}; \\ B\backslash A= \{ x \in B| x \notin A\}.\)
Lời giải:
a) \( A=\{x \in \mathbb R | -4 \le x \le 4 \} = \left[ { – 4;4} \right], \quad B = \left( { – 3;8} \right].\)
b)
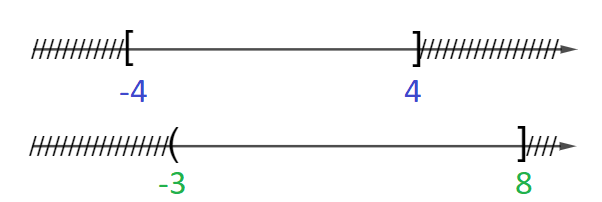
\(A \cap B = \left( { – 3;4} \right],\quad A\backslash B = \left[ { – 4; – 3} \right],\quad B\backslash A = \left( {4;8} \right].\)