Trả lời LG a Bài 6. Hệ thức lượng trong tam giác (trang 42) – SGK Toán 10 Kết nối tri thức. Gợi ý: Bước 1: Vẽ hình mô tả đường đi từ cảng A.
Câu hỏi/Đề bài:
Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu
Hướng dẫn:
Bước 1: Vẽ hình mô tả đường đi từ cảng A, đến nơi mà động cơ hỏng (kí hiệu là B) và hòn đảo (kí hiệu là C) nơi tàu neo đậu.
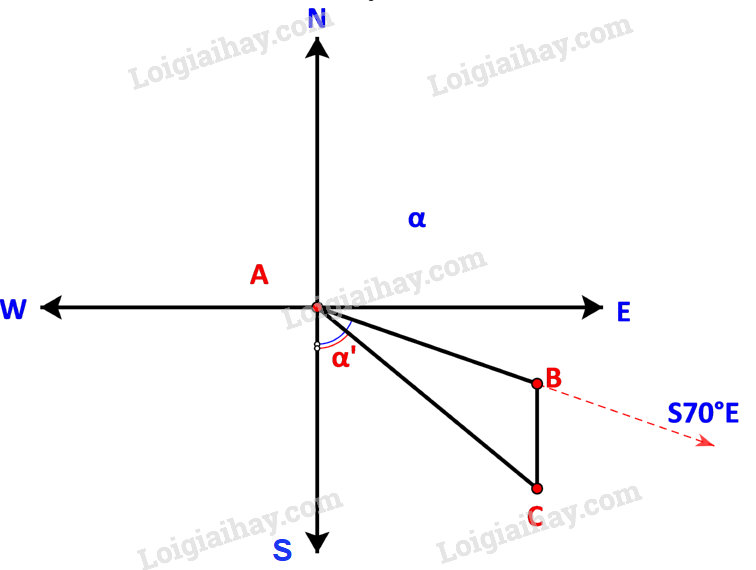
Bước 2: Tính góc \(\widehat {ABC}\), quãng đường tàu đi được sau 90 phút () và quãng đường tàu trôi tự do ().
Bước 3: Tính khoảng cách từ cảng tới nơi tàu neo đậu (đoạn AC) bằng cách áp dụng định lí cosin tại đỉnh B.
Lời giải:
Ta có sơ đồ đường đi như sau:
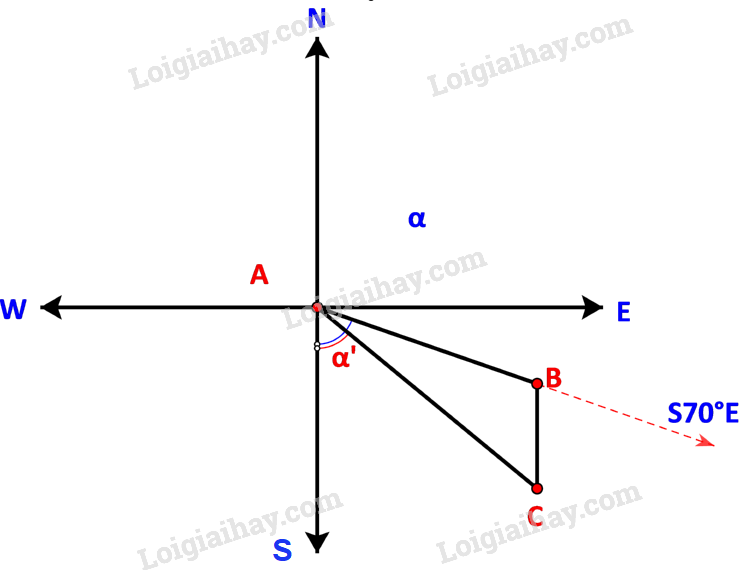
Trong đó: B là nơi động cơ bị hỏng, C là ví trí neo đậu của tàu trên hòn đảo.
Khoảng cách từ cảng A tới đảo nơi tàu neo đậu là đoạn AC.
Quãng đường tàu đi được sau 90 phút hay 1,5 giờ (ngay trước khi hỏng động cơ) là:
70.1,5 = 105 (km) hay AB = 105.
Sau 2 giờ tàu trôi tự do từ B đến C với vận tốc 8km/h , suy ra BC= 8.2 = 16 (km).
Ban đầu tàu di chuyển theo hướng \(S{70^o}E\) nên \(\widehat {BAS} = {70^o}\). Sau khi động cơ bị hỏng, tàu trôi theo hướng Nam do đó BC song song với AS.
\( \Rightarrow \widehat {ABC} = {180^o} – \widehat {BAS} = {110^o}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\({AC^2} = {BC^2} + {AB^2} – 2.AC.BC.\cos B\)
\(\begin{array}{l} \Rightarrow {AC^2} = {16^2} + {105^2} – 2.16.105.\cos {110^o} \approx 12430\\ \Rightarrow AC \approx 111,5.\end{array}\)
Vậy khoảng cách từ cảng A tới đảo nơi tàu neo đậu là khoảng 111,5 km.