Lời giải Hoạt động 2 Bài 10. Vectơ trong mặt phẳng tọa độ (trang 60, 61) – SGK Toán 10 Kết nối tri thức. Hướng dẫn: Quy tắc hình bình hành.
Câu hỏi/Đề bài:
Trong Hình 4.33:
a) Hãy biểu thị mỗi vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
b) Hãy biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) từ đó biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
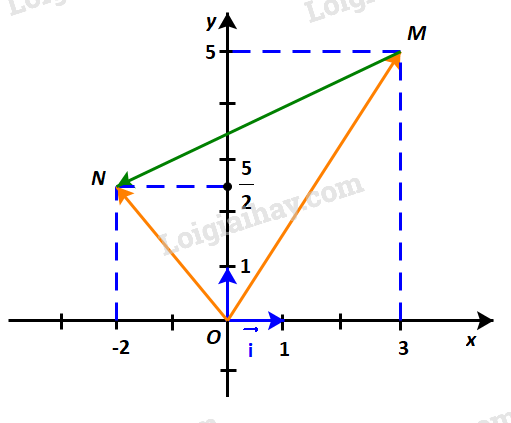
Hướng dẫn:
a) Quy tắc hình bình hành:
Tứ giác OAMB là hình bình hành thì \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \)
b) Quy tắc hiệu: \(\overrightarrow {MN} = \overrightarrow {ON} – \;\overrightarrow {OM} \)
Lời giải:
Dựng hình bình hành OAMB và OCND như hình dưới:
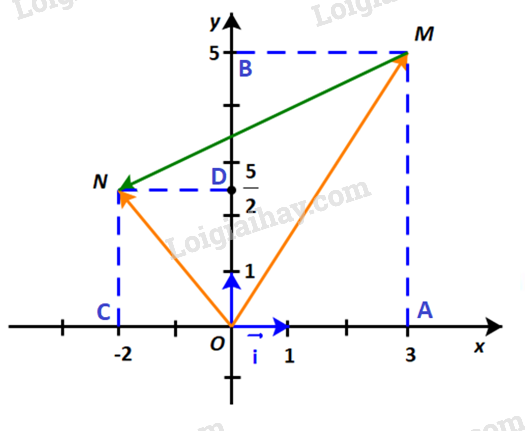
Khi đó: \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \) và \(\overrightarrow {ON} = \overrightarrow {OC} + \overrightarrow {OD} \).
Dễ thấy:
\(\overrightarrow {OA} = 3\;\overrightarrow i ;\;\,\overrightarrow {OB} = 5\;\overrightarrow j \) và \(\overrightarrow {OC} = – 2\;\overrightarrow i ;\;\,\overrightarrow {OD} = \frac{5}{2}\;\overrightarrow j \)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {OM} = 3\;\overrightarrow i + 5\;\overrightarrow j \\\overrightarrow {ON} = – 2\;\overrightarrow i + \frac{5}{2}\;\overrightarrow j \end{array} \right.\)
b) Ta có: \(\overrightarrow {MN} = \overrightarrow {ON} – \;\overrightarrow {OM} \) (quy tắc hiệu)
\(\begin{array}{l} \Rightarrow \overrightarrow {MN} = \left( { – 2\;\overrightarrow i + \frac{5}{2}\;\overrightarrow j } \right) – \left( {\;3\;\overrightarrow i + 5\;\overrightarrow j } \right)\\ \Leftrightarrow \overrightarrow {MN} = \left( { – 2\;\overrightarrow i – 3\;\overrightarrow i } \right) + \left( {\frac{5}{2}\;\overrightarrow j – 5\;\overrightarrow j } \right)\\ \Leftrightarrow \overrightarrow {MN} = – 5\;\overrightarrow i – \frac{5}{2}\;\overrightarrow j \end{array}\)
Vậy \(\overrightarrow {MN} = – 5\;\overrightarrow i – \frac{5}{2}\;\overrightarrow j \).