Định lí cosin trong tam giác OAC: \(A{C^2} = O{A^2} + O{C^2} – 2. OA. OC. \cos \widehat {AOC}\. Hướng dẫn giải Giải bài 4.39 trang 72 SGK Toán 10 – Kết nối tri thức – Bài tập cuối Chương 4. Trên sông, một cano chuyển động thẳng đều theo hướng S15E với vận tốc có độ lớn bằng 20 km/h….
Đề bài/câu hỏi:
Trên sông, một cano chuyển động thẳng đều theo hướng \(S{15^o}E\) với vận tốc có độ lớn bằng 20 km/h. Tính vận tốc riêng của cano, biết rằng, nước trên sông chảy về hướng đông với vận tốc có độ lớn bằng 3 km/h.
Hướng dẫn:
Định lí cosin trong tam giác OAC: \(A{C^2} = O{A^2} + O{C^2} – 2.OA.OC.\cos \widehat {AOC}\)
Lời giải:
Lấy các điểm: A, C sao cho:
Vectơ vận tốc dòng nước\(\overrightarrow {{v_n}} = \overrightarrow {OA} \)
Vectơ vận tốc chuyển động \(\overrightarrow {{v_{cano}}} = \overrightarrow {OC} \)
Ta có: \(\overrightarrow {{v_{cano}}} = \overrightarrow {{v_n}} + \overrightarrow v \), với \(\overrightarrow v \) là vectơ vận tốc riêng của cano.
Gọi B là điểm sao cho \(\overrightarrow v = \overrightarrow {OB} \) thì OACB là hình bình hành.
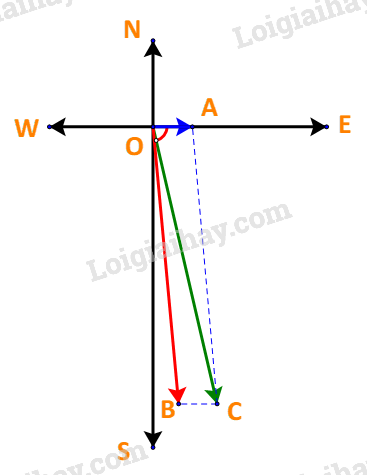
Vì tàu chuyển động theo hướng \(S{15^o}E\) nên vectơ \(\overrightarrow {OC} \) tạo với hướng Nam (tia OS) góc \({15^o}\) và tạo với hướng Đông (tia OE) góc \({90^o} – {15^o} = {75^o}\).
Mà nước trên sông chảy về hướng đông nên vectơ \(\overrightarrow {OA} \) cùng hướng với vectơ \(\overrightarrow {OE} \)
Do đó góc tạo bởi vectơ \(\overrightarrow {OC} \) và vectơ \(\overrightarrow {OA} \) là \({75^o}\)
Xét tam giác OAC ta có:
\(OA = \;|\overrightarrow {{v_n}} |\; = 3\); \(OC = \;|\overrightarrow {{v_{cano}}} |\; = 20\) và \(\widehat {AOC} = {75^o}\)
Áp dụng định lí cosin tại đỉnh O ta được:
\(\begin{array}{l}A{C^2} = O{A^2} + O{C^2} – 2.OA.OC.\cos \widehat {AOC}\\ \Leftrightarrow A{C^2} = {3^2} + {20^2} – 2.3.20.\cos {75^o} \approx 378\\ \Leftrightarrow OB = AC \approx 19,44\end{array}\)
Vậy vận tốc riêng của cano là 19,44 km/h