Thu gọn bất phương trình về dạng tổng quát. Biểu diễn miền nghiệm của bất phương trình: Bước 1: Vẽ đường thẳng (nét liền). Lời giải bài tập, câu hỏi Giải bài 2.12 trang 32 SGK Toán 10 tập 1 – Kết nối tri thức – Bài tập cuối Chương 2. Biểu diễn miền nghiệm của bất phương trình trên mặt phẳng tọa độ….
Đề bài/câu hỏi:
Biểu diễn miền nghiệm của bất phương trình \(\dfrac{{x + y}}{2} \ge \dfrac{{2x – y + 1}}{3}\) trên mặt phẳng tọa độ.
Hướng dẫn:
Thu gọn bất phương trình về dạng tổng quát.
Biểu diễn miền nghiệm của bất phương trình:
Bước 1: Vẽ đường thẳng (nét liền).
Bước 2: Lấy một điểm bất kì không thuộc d trên mặt phẳng rồi thay vào biểu thức ax+b. Xác định c có bằng 0 hay không, nếu c = 0 thì ta lấy điểm A(-1;-1) để thay vào.
Nếu A thỏa mãn bất phương trình thì miền nghiệm của bất phương trình đã cho là nửa mặt phẳng bờ d chứa điểm A đã lấy.
Lời giải:
\(\begin{array}{l}\dfrac{{x + y}}{2} \ge \dfrac{{2x – y + 1}}{3}\\ \Leftrightarrow 3\left( {x + y} \right) \ge 2\left( {2x – y + 1} \right)\\ \Leftrightarrow 3x + 3y \ge 4x – 2y + 2\\ \Leftrightarrow x – 5y \le – 2\end{array}\)
Biểu diễn miền nghiệm của bất phương trình:
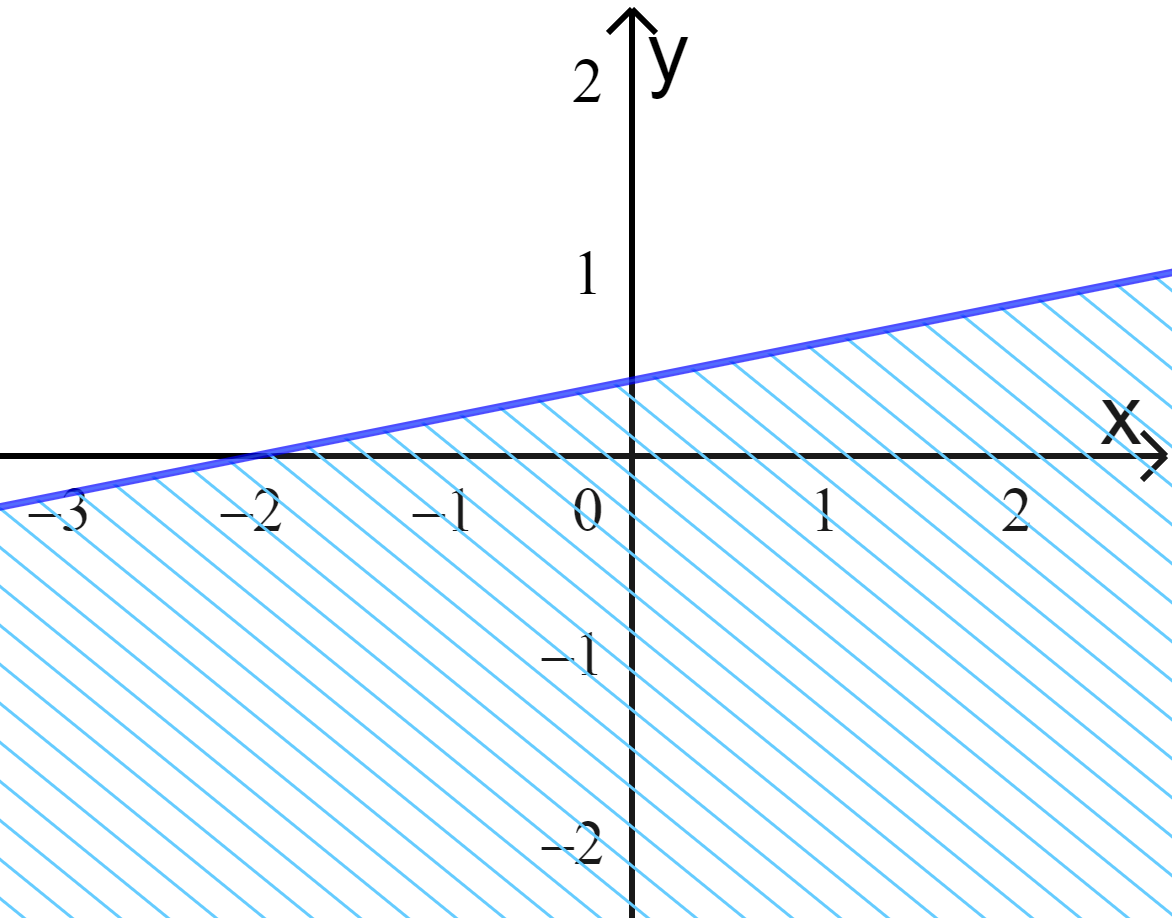
Bước 1: Vẽ đường thẳng d:\(x – 5y = – 2\) (nét liền) đi qua A(-2;0) và B(0;0,4)
Bước 2: Lấy tọa độ điểm O(0;0) thay vào biểu thức x-5y ta được: x-5y=0-5.0=0>-2
=> Điểm O không thuộc miền nghiệm của bất phương trình.
Vậy miền nghiệm của BPT đã cho là nửa mặt phẳng có bờ là đường thẳng d:\(x – 5y = – 2\) và không chứa gốc tọa độ O.