\(A \cap B = \left\{ {x \in A|\;x \in B} \right\}\) \(A\;{\rm{\backslash }}\;B = \left\{ {x \in A|\;x \notin B} \right\}\. Lời giải Giải bài 1.21 trang 20 SGK Toán 10 tập 1 – Kết nối tri thức – Bài tập cuối Chương 1. Cho tập hợp A,B được mình họa bằng biểu đồ Ven như hình bên….
Đề bài/câu hỏi:
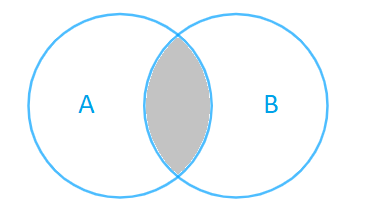
Cho tập hợp A,B được mình họa bằng biểu đồ Ven như hình bên. Phần tô màu xám trong hình là biểu diễn của tập hợp nào sau đây?
A. \(A \cap B\)
B. \(A\;{\rm{\backslash }}\;B\)
C. \(A \cup B\)
D. \(B\;{\rm{\backslash }}\;A\)
Hướng dẫn:
\(A \cap B = \left\{ {x \in A|\;x \in B} \right\}\)
\(A\;{\rm{\backslash }}\;B = \left\{ {x \in A|\;x \notin B} \right\}\)
\(A \cup B = \) {\(x \in A\) hoặc \(x \in B\)}
\(B\;{\rm{\backslash }}\;A = \left\{ {x \in B|\;x \notin A} \right\}\)
Lời giải:
Phần màu xám là phần giao nhau giữa tập hợp A và tập hợp B: vừa thuộc A, vừa thuộc B.
Do đó phần màu xám là \(A \cap B\)
Chọn đáp án A