Giải Vận dụng 2 Bài 4. Ba đường conic trong mặt phẳng tọa độ (trang 65, 66, 67) – SGK Toán 10 Chân trời sáng tạo. Tham khảo: Bước 1: Xác định khoảng cách từ tâm đến đỉnh tháp và đáy tháp.
Câu hỏi/Đề bài:
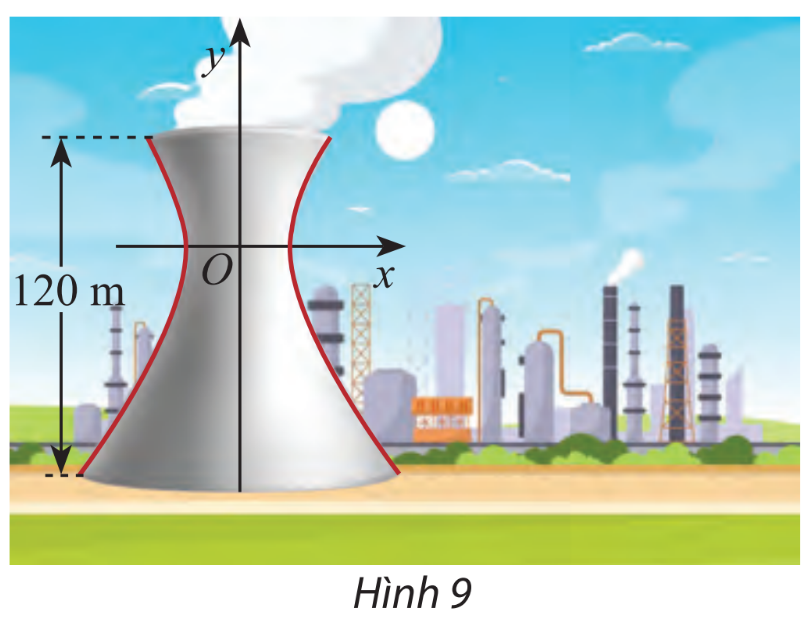
Một tháp làm nguội của một nhà cát có mặt cắt là một hypebol có phương trình \(\frac{{{x^2}}}{{{{27}^2}}} – \frac{{{y^2}}}{{{{40}^2}}} = 1\) (hình 9). Cho biết chiều cao của tháp là 120 m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng một nửa khoảng cách từ tâm đối xứng đến đáy. Tìm bán kính đường tròn nóc và bán kính đường tròn đáy của tháp.
Hướng dẫn:
Bước 1: Xác định khoảng cách từ tâm đến đỉnh tháp và đáy tháp
Bước 2: Từ kết quả vừa tìm thay vào phương trình hypebol y bằng kết quả đó tìm x (Chỉ lấy kết quả dương)
Lời giải:
Gọi khoảng cách từ tâm đối xứng đến đỉnh tháp là z
Suy ra khoảng cách từ tâm đối xứng đến đáy tháp là 2z
Ta có \(z + 2z = 120 \Rightarrow z = 40\)
Thay \(y = 40\) vào phương trình \(\frac{{{x^2}}}{{{{27}^2}}} – \frac{{{y^2}}}{{{{40}^2}}} = 1\) ta tìm được \(x = 27\sqrt 2 \)
Thay \(y = 80\) vào phương trình \(\frac{{{x^2}}}{{{{27}^2}}} – \frac{{{y^2}}}{{{{40}^2}}} = 1\) ta tìm được \(x = 27\sqrt 5 \)
Vậy bán kính đường tròn nóc và bán kính đường tròn đáy của tháp lần lượt là \(27\sqrt 2 \) và \(27\sqrt 5 \)