Lời giải Thực hành 1 Bài 1. Giá trị lượng giác của một góc từ 0 đến 180 (trang 61, 62) – SGK Toán 10 Chân trời sáng tạo. Gợi ý: Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^o}\.
Câu hỏi/Đề bài:
Tìm các giá trị lượng giác của góc \({135^o}\)
Hướng dẫn:
Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^o}\)
Khi đó hoành độ và tung độ của điểm M lần lượt là các giá trị \(\cos {135^o},\;\sin {135^o}\)
Từ đó suy ra\(\;\tan {135^o} = \frac{{\sin {{135}^o}}}{{\cos {{135}^o}}},\;\;\cot {135^o} = \frac{{\cos {{135}^o}}}{{\sin {{135}^o}}}.\)
Lời giải:
Lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^o}\), H là hình chiếu vuông góc của M trên Oy.
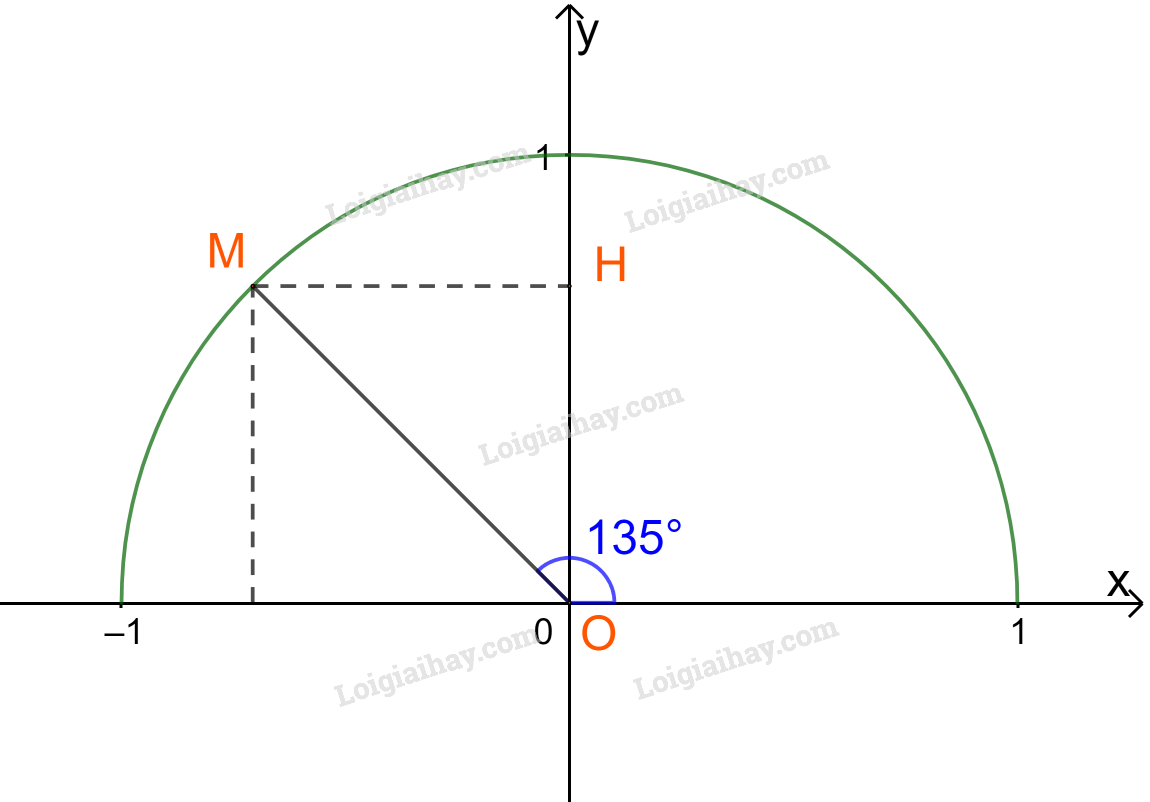
Ta có: \(\widehat {MOy} = {135^o} – {90^o} = {45^o}\).
Tam giác OMH vuông cân tại H nên \(OH = MH = \frac{{OM}}{{\sqrt 2 }} = \frac{1}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{2}.\)
Vậy tọa độ điểm M là \(\left( { – \frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right).\)
Vậy theo định nghĩa ta có:
\(\begin{array}{l}\;\sin {135^o} = \frac{{\sqrt 2 }}{2};\;\;\cos {135^o} = – \frac{{\sqrt 2 }}{2};\\\;\tan {135^o} = – 1;\;\;\cot {135^o} = – 1.\end{array}\)
Chú ý
Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc \({135^o}\)
Với các loại máy tính fx-570 ES (VN hoặc VN PLUS) ta làm như sau:
Bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ)
Tính \(\sin {135^o}\), bấm phím: sin 1 3 5 \(^o\)’’’ = ta được kết quả là \(\frac{{\sqrt 2 }}{2}\)
Tính \(\cos {135^o}\),bấm phím: cos 1 3 5 \(^o\)’’’ = ta được kết quả là \(\frac{{ – \sqrt 2 }}{2}\)
Tính \(\tan {135^o}\), bấm phím: tan 1 3 5 \(^o\)’’’ = ta được kết quả là \( – 1\)
(Để tính \(\cot {135^o}\), ta tính \(1:\tan {135^o}\))