Giải chi tiết Hoạt động Khám phá 6 Bài 4. Ba đường conic trong mặt phẳng tọa độ (trang 68, 69, 70) – SGK Toán 10 Chân trời sáng tạo. Gợi ý: Sử dụng phương pháp tọa độ trong mặt phẳng.
Câu hỏi/Đề bài:
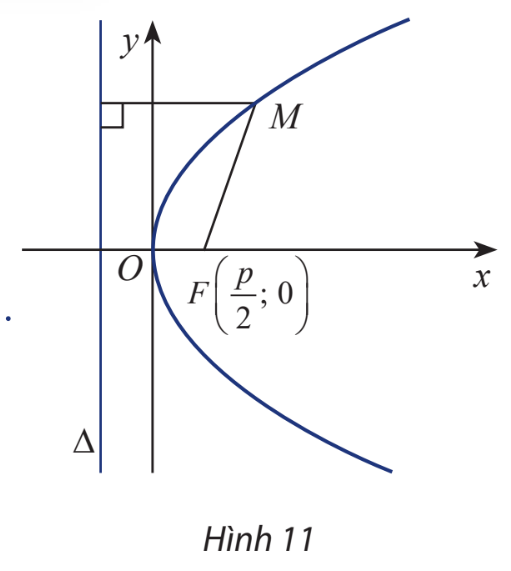
Cho parabol (P) có tiêu điểm F và đường chuẩn \(\Delta \). Gọi khoảng cách từ tiêu điểm đến đường chuẩn là p, hiển nhiên \(p > 0\)
Chọn hệ trục tọa độ Oxy sao cho \(F\left( {\frac{p}{2};0} \right)\) và \(\Delta :x + \frac{p}{2} = 0\)
Xét điểm \(M(x;y)\)
a) Tính MF và \(d\left( {M,\Delta } \right)\)
b) Giải thích biểu thức sau:
\(M(x;y) \in (P) \Leftrightarrow \sqrt {{{\left( {x – \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|\)
Hướng dẫn:
Sử dụng phương pháp tọa độ trong mặt phẳng
Lời giải:
a) Ta có: \(\overrightarrow {FM} = \left( {x – \frac{p}{2};y} \right) \Rightarrow MF = \left| {\overrightarrow {FM} } \right| = \sqrt {{{\left( {x – \frac{p}{2}} \right)}^2} + {y^2}} \)
\(d\left( {M,\Delta } \right) = \frac{{\left| {x + \frac{p}{2}} \right|}}{1} = \left| {x + \frac{p}{2}} \right|\)
b) M thuộc parabol (P) nên M cách đều F và \(\Delta \)
Suy ra \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{{\left( {x – \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x – \frac{p}{2}} \right|\)