Bài 9 trang 103 Toán 10 tập 1 – Chân trời sáng tạo: Một chiếc máy bay được biết là đang bay về phía Bắc với tốc độ 45m/s

Đề bài/câu hỏi:

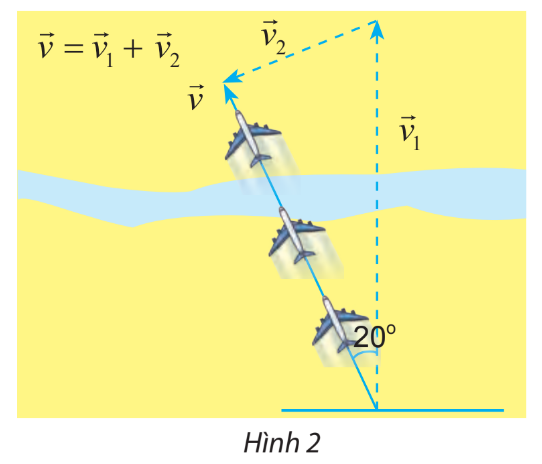
Một chiếc máy bay được biết là đang bay về phía Bắc với tốc độ \(45\)m/s, mặc dù vận tốc của nó so với mặt đất là 38 m/s theo hướng nghiêng một góc \(20^\circ \) về phía tây bắc (hình 2). Tính tốc độ của gió

Hướng dẫn:

Bước 1: Dựa vào hình 2 xác định các vectơ tương ứng với vận tốc của máy bay, vận tốc so với mặt đất

Bước 2: Dựa vào mối liên hệ giữa các vectơ đã cho \(\overrightarrow v = \overrightarrow {{v_1}} + \overrightarrow {{v_2}} \) xác định vectơ tương ứng với vận tốc gió

Bước 3: Áp dụng định lý cosin tìm tốc độ của gió

Lời giải:

Từ giả thiết ta có:

+) Vectơ tương ứng với vận tốc máy bay là vectơ \(\overrightarrow {{v_1}} \)

+) Vectơ tương ứng với vận tốc máy bay so với mặt đất là vectơ \(\overrightarrow v \)

+) Vectơ tương ứng với vận tốc gió là vectơ \(\overrightarrow {{v_2}} \)

Ta có : \(\left| {\overrightarrow {{v_1}} } \right| = 45;\left| {\overrightarrow v } \right| = 38;\left( {\overrightarrow {{v_1}} ,\overrightarrow v } \right) = 20^\circ \)

Áp dụng định lý cosin ta có:

\(\left| {\overrightarrow {{v_2}} } \right| = \sqrt {{{\left| {\overrightarrow v } \right|}^2} + {{\left| {\overrightarrow {{v_1}} } \right|}^2} – 2\left| {\overrightarrow v } \right|.\left| {\overrightarrow {{v_1}} } \right|.\cos \left( {\overrightarrow v ,\overrightarrow {{v_1}} } \right)} \)

\( = \sqrt {{{38}^2} + {{45}^2} – 2.38.45.\cos 20^\circ } \simeq 16\) (m/s)

Vậy tốc độ của gió gần bằng 16 m/s