Bài 6 trang 25 Toán 10 tập 1 – Chân trời sáng tạo: Xác định các tập hợp sau đây: a) ( – ∇ ;0] ∪ [ – π ;π ] b) [ – 3, 5;2] ∩ ( – 2;3, 5)

Đề bài/câu hỏi:

Xác định các tập hợp sau đây:

a) \(( – \infty ;0] \cup [ – \pi ;\pi ]\)

b) \([ – 3,5;2] \cap ( – 2;3,5)\)

c) \(( – \infty ;\sqrt 2 ] \cap [1; + \infty )\)

d) \(( – \infty ;\sqrt 2 ]{\rm{\backslash }}[1; + \infty )\)

Hướng dẫn:

Biểu diễn các tập hợp trên trục số

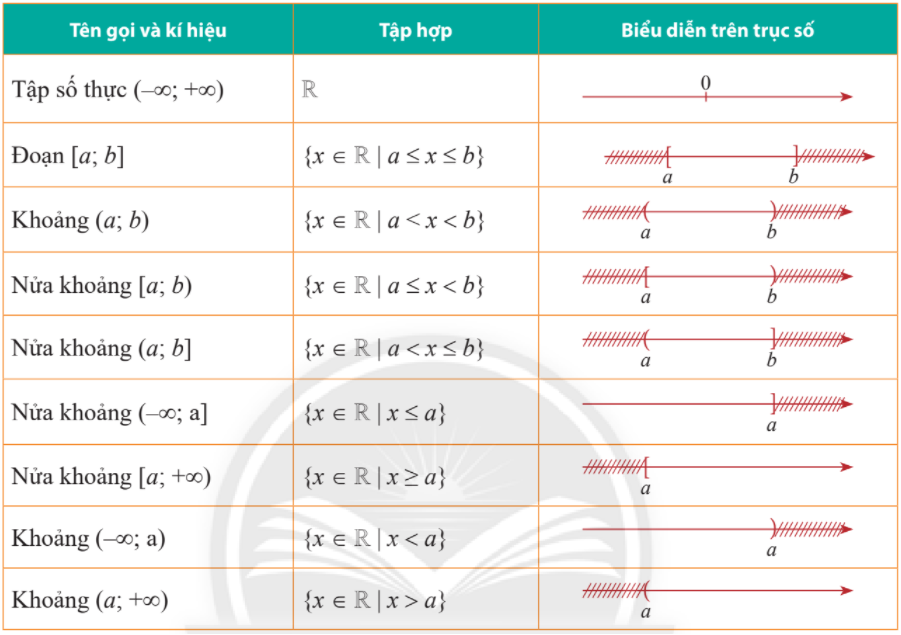
Lời giải:

a) Để xác định tập hợp \(A = ( – \infty ;0] \cup [ – \pi ;\pi ]\), ta vẽ sơ đồ sau đây:

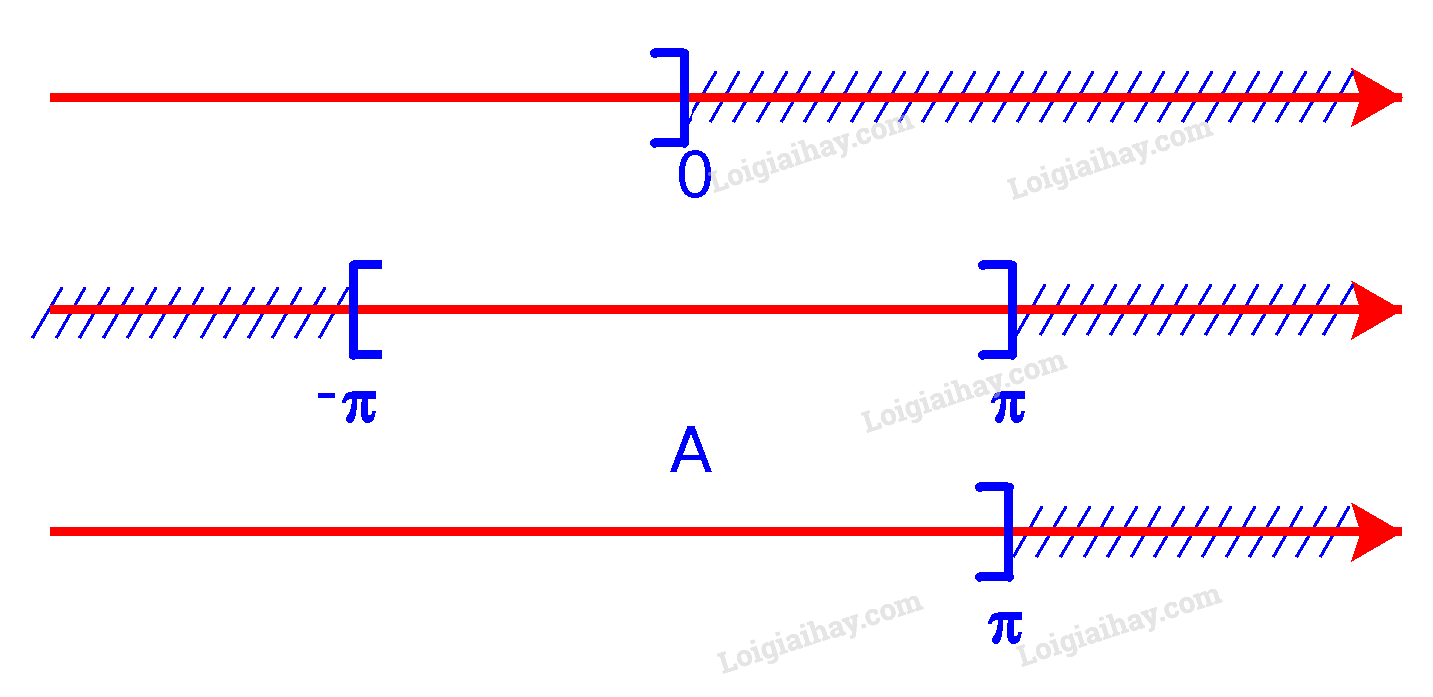
Từ sơ đồ, ta thấy \(A = ( – \infty ;\pi ]\)

b) Để xác định tập hợp \(B = [ – 3,5;2] \cap ( – 2;3,5)\), ta vẽ sơ đồ sau đây:

Từ sơ đồ, ta thấy \(B = ( – 2;2]\)

c) Để xác định tập hợp \(C = ( – \infty ;\sqrt 2 ] \cap [1; + \infty )\), ta vẽ sơ đồ sau đây:

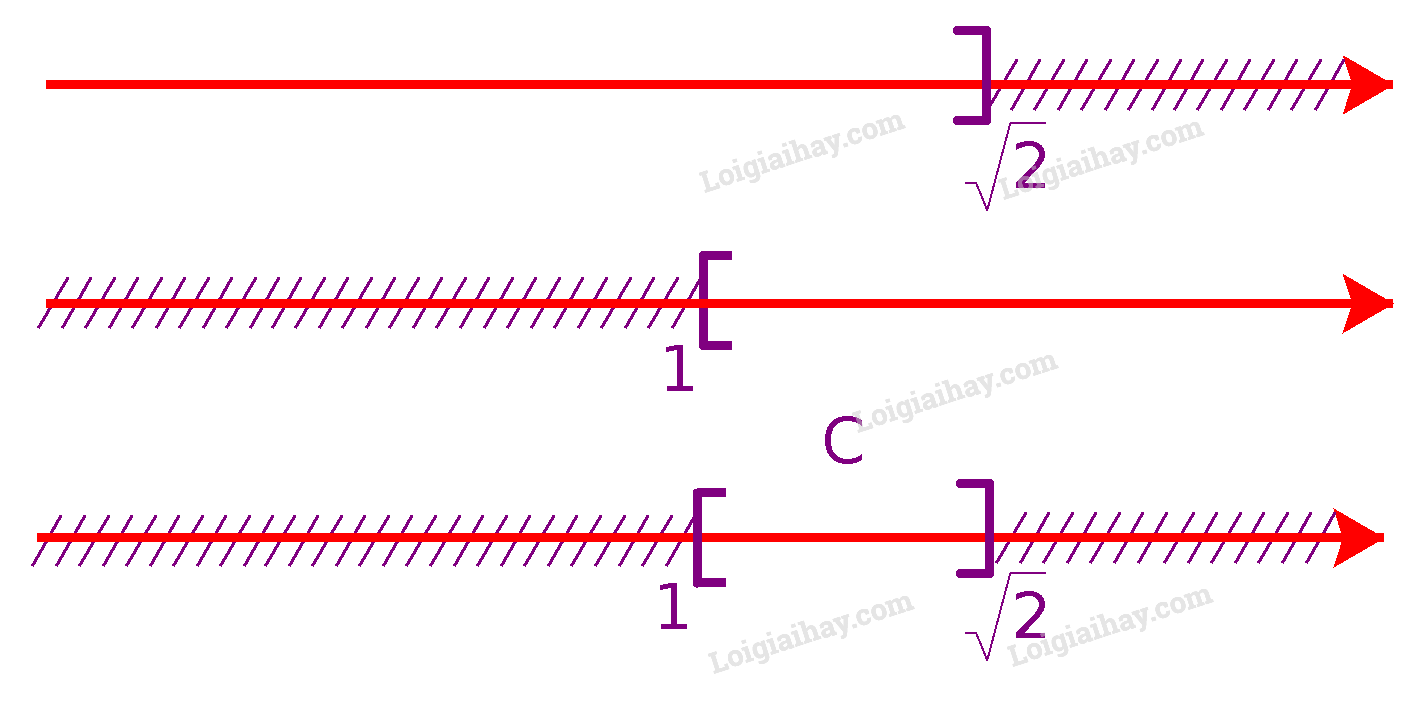
Từ sơ đồ, ta thấy \(C = [1;\sqrt 2 ]\)

d) Để xác định tập hợp \(D = ( – \infty ;\sqrt 2 ]{\rm{\backslash }}[1; + \infty )\), ta vẽ sơ đồ sau đây:

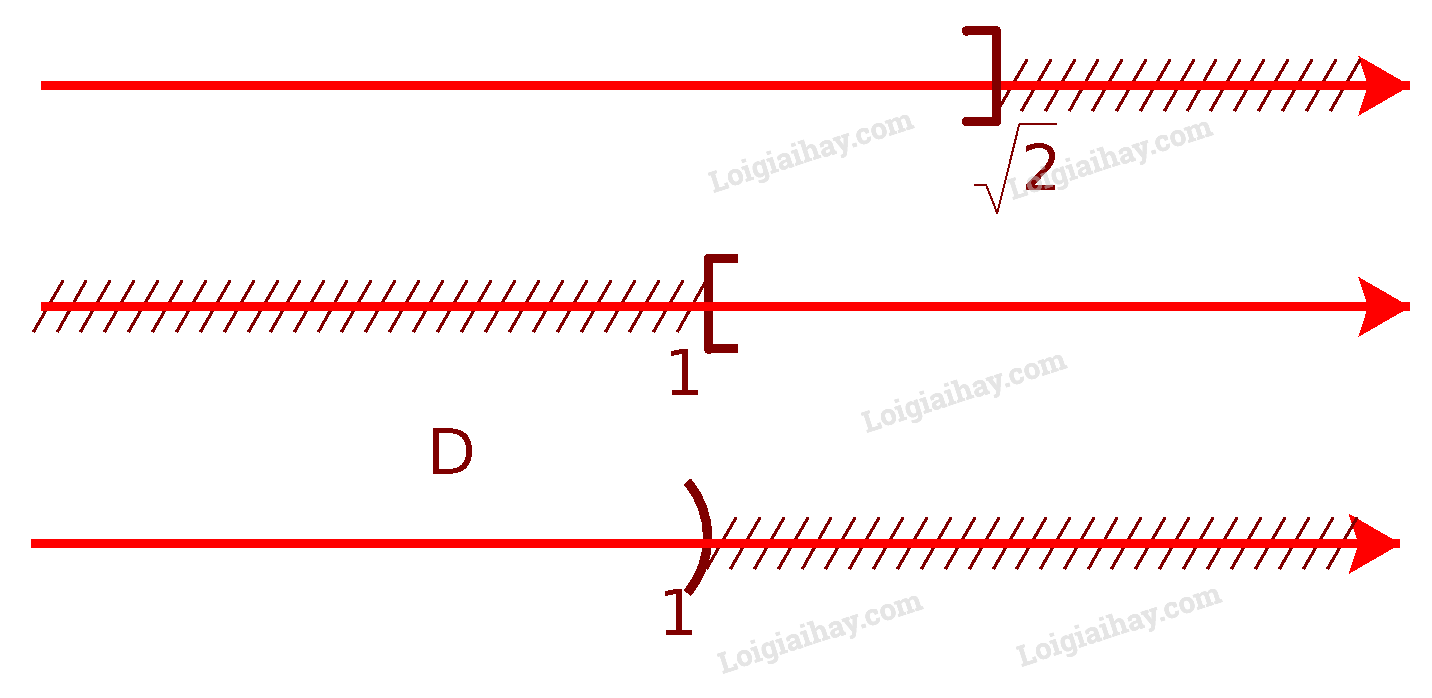
Từ sơ đồ, ta thấy \(D = ( – \infty ;1)\)