Gọi x, y lần lượt là số kilogam sản phẩm loại A, loại B mà công ty đó sản xuất. Gợi ý giải Giải bài 3 trang 39 SGK Toán 10 tập 1 – Chân trời sáng tạo – Bài tập cuối Chương 2. Một công ty dự định sản xuất hai loại sản phẩm A và B….
Đề bài/câu hỏi:
Một công ty dự định sản xuất hai loại sản phẩm A và B. Các sản phẩm này được chế tạo từ ba loại nguyên liệu I, II và III. Số kilôgam dự trữ từng loại nguyên liệu và số kilôgam từng loại nguyên liệu cần dùng để sản xuất ra 1 kg sản phẩm được cho trong bảng sau:
|
Loại nguyên liệu |
Số kilogam nguyên liệu dự trữ |
Số kilogam nguyên liệu cần dùng sản xuất 1 kg sản phẩm |
|
|
A |
B |
||
|
I |
8 |
2 |
1 |
|
II |
24 |
4 |
4 |
|
III |
8 |
1 |
2 |
Công ty đó nên sản xuất bao nhiêu sản phẩm mỗi loại để tiền lãi thu về lớn nhất? Biết rằng, mỗi kilôgam sản phẩm loại A lãi 30 triệu đồng, mỗi kilôgam sản phẩm loại B lãi 50 triệu đồng.
Hướng dẫn:
Gọi x, y lần lượt là số kilogam sản phẩm loại A, loại B mà công ty đó sản xuất.
Lập các điều kiện ràng buộc đối với x, y thành hệ bất phương trình
Biểu diễn miền nghiệm của mỗi bất phương trình trên cùng một hệ trục tọa độ Oxy
Lời giải:
Gọi x, y lần lượt là số kilogam sản phẩm loại A, loại B mà công ty đó sản xuất.
Ta có các điều kiện ràng buộc đối với x, y như sau:
– Hiển nhiên \(x \ge 0,y \ge 0\)
– Nguyên liệu loại I có số kilogam dự trữ là 8 kg nên \(2x + y \le 8\)
– Nguyên liệu loại II có số kilogam dự trữ là 24 kg nên \(4x + 4y \le 24\)
– Nguyên liệu loại III có số kilogam dự trữ là 8 kg nên \(x + 2y \le 8\)
Từ đó ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}2x + y \le 8\\4x + 4y \le 24\\x + 2y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên hệ trục tọa độ Oxy.
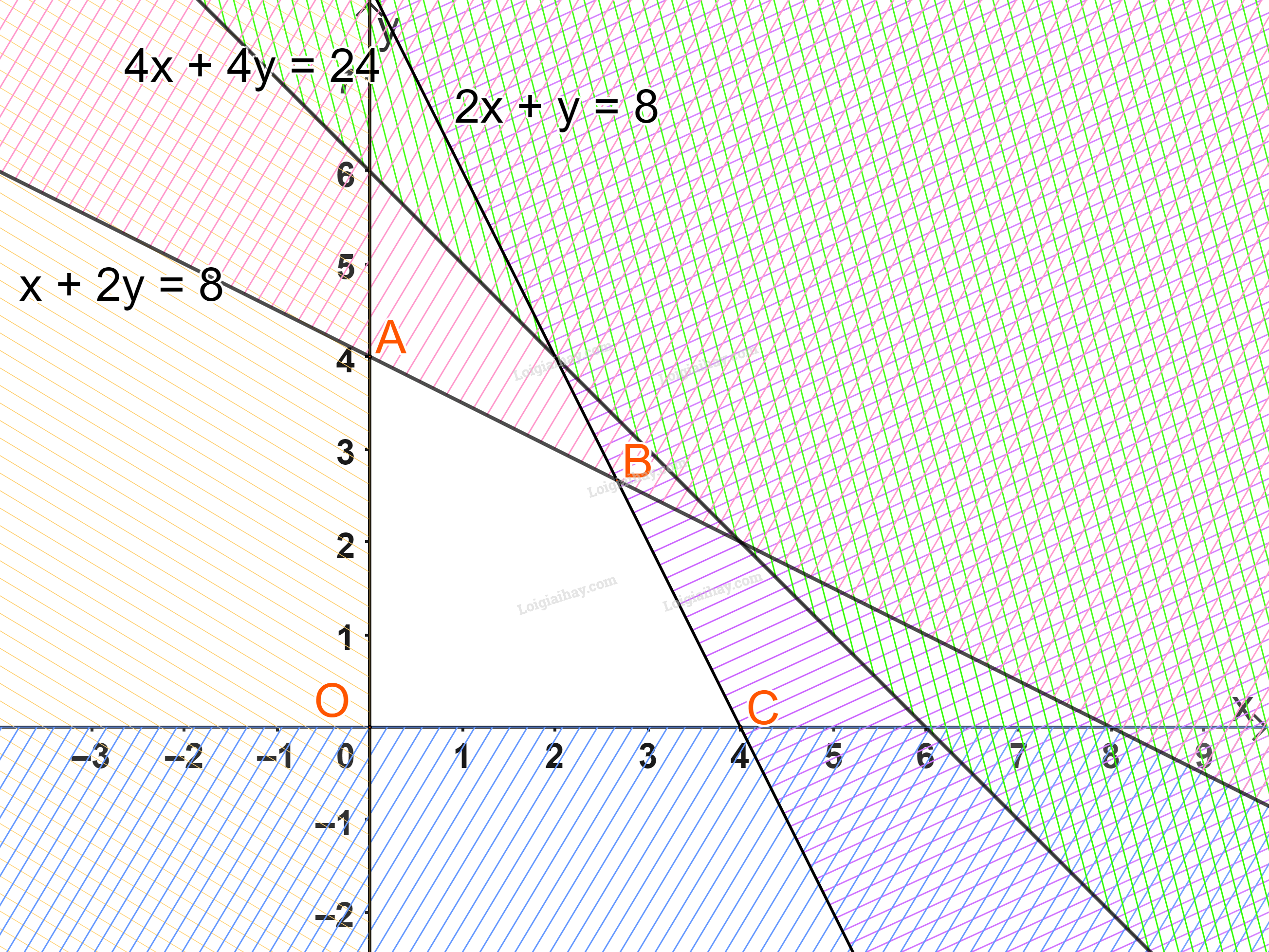
Miền không gạch chéo (miền tứ giác OABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
Với các đỉnh \(O(0;0),A(0;4),\)\(B(\frac{8}{3};\frac{8}{3}),\)\(C(4;0).\)
Gọi F là số tiền lãi (đơn vị: triệu đồng) thu về, ta có: \(F = 30x + 50y\)
Tính giá trị của F tại các đỉnh của tứ giác:
Tại \(O(0;0),\)\(F = 30.0 + 50.0 = 0\)
Tại \(A(0;4),\)\(F = 30.0 + 50.4 = 200\)
Tại \(B(\frac{8}{3};\frac{8}{3}),\)\(F = 30.\frac{8}{3} + 50.\frac{8}{3} = \frac{{640}}{3}\)
Tại \(C(4;0):\)\(F = 30.4 + 50.0 = 120\)
F đạt giá trị lớn nhất bằng \(\frac{{640}}{3}\) tại \(B(\frac{8}{3};\frac{8}{3}).\)
Vậy công ty đó nên sản xuất \(\frac{8}{3}kg\)sản phẩm mỗi loại để tiền lãi thu về lớn nhất.