Chèn điểm M: \(\overrightarrow {AB} = \overrightarrow {AM} + \overrightarrow {MB} \), Tính chất trung điểm \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \. Phân tích, đưa ra lời giải Giải bài 2 trang 97 SGK Toán 10 tập 1 – Chân trời sáng tạo – Bài 3. Tích của một số với một vectơ. Cho tứ giác ABCD gọi M và N lần lượt là trung điểm của các cạnh AB và CD ….
Đề bài/câu hỏi:
Cho tứ giác ABCD gọi M và N lần lượt là trung điểm của các cạnh AB và CD . Chứng minh rằng
a) \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN} \)
b) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
Hướng dẫn:
Chèn điểm M: \(\overrightarrow {AB} = \overrightarrow {AM} + \overrightarrow {MB} \),
Tính chất trung điểm \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 \)
Lời giải:
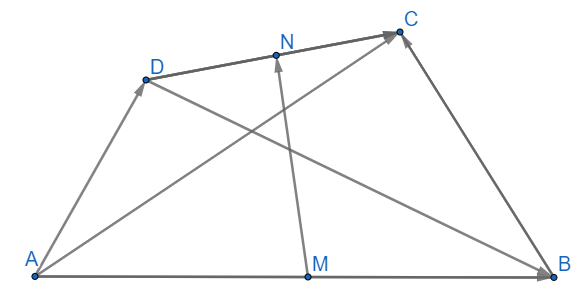
a) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {ND} \\= \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) \\= \overrightarrow 0 + 2\overrightarrow {MN} + \overrightarrow 0 = 2\overrightarrow {MN} \) (đpcm)
b) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
\(\)\(\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND} \)
\(\left( {\overrightarrow {BM} + \overrightarrow {AM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) = 2\overrightarrow {MN} \)
Mặt khác ta có: \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN} \)
Suy ra \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
Cách 2:
\(\begin{array}{l}\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \\ \Leftrightarrow \overrightarrow {AC} – \overrightarrow {AD} = \overrightarrow {BC} – \overrightarrow {BD} \\ \Leftrightarrow \overrightarrow {DC} = \overrightarrow {DC} (đpcm)\end{array}\)