Bước 1: Gắn hệ trục tọa độ Oxy Bước 2: Gọi phương trình chính tắc mô phỏng cổng là \({y^2} = 2px\) Bước 3. Giải chi tiết Giải bài 17 trang 75 SGK Toán 10 tập 2 – Chân trời sáng tạo – Bài tập cuối Chương 9. Cổng trời của một thành phố dạng hình parabol có khoảng cách giữa hai chân cổng là 192 m (hình…
Đề bài/câu hỏi:
Cổng trời của một thành phố dạng hình parabol có khoảng cách giữa hai chân cổng là 192 m (hình 3). Từ một điểm M trên thân cổng, người ta đo được khoảng cách đến mặt đất là 2 m và khoảng cách từ chân đường vuông góc kẻ từ M xuống mặt đất đến chân cổng gần nhất là 0,5 m. Tính chiều cao của cổng
Hướng dẫn:
Bước 1: Gắn hệ trục tọa độ Oxy
Bước 2: Gọi phương trình chính tắc mô phỏng cổng là \({y^2} = 2px\)
Bước 3: Thay điểm M vào phương trình, xác định phương trình parabol
Bước 4: Xác định chiều cao của cổng
Lời giải:
Gắn hệ trục Oxy vào chiếc cổng, gọi chiều cao của cổng là h ta vẽ lại parabol như dưới đây:
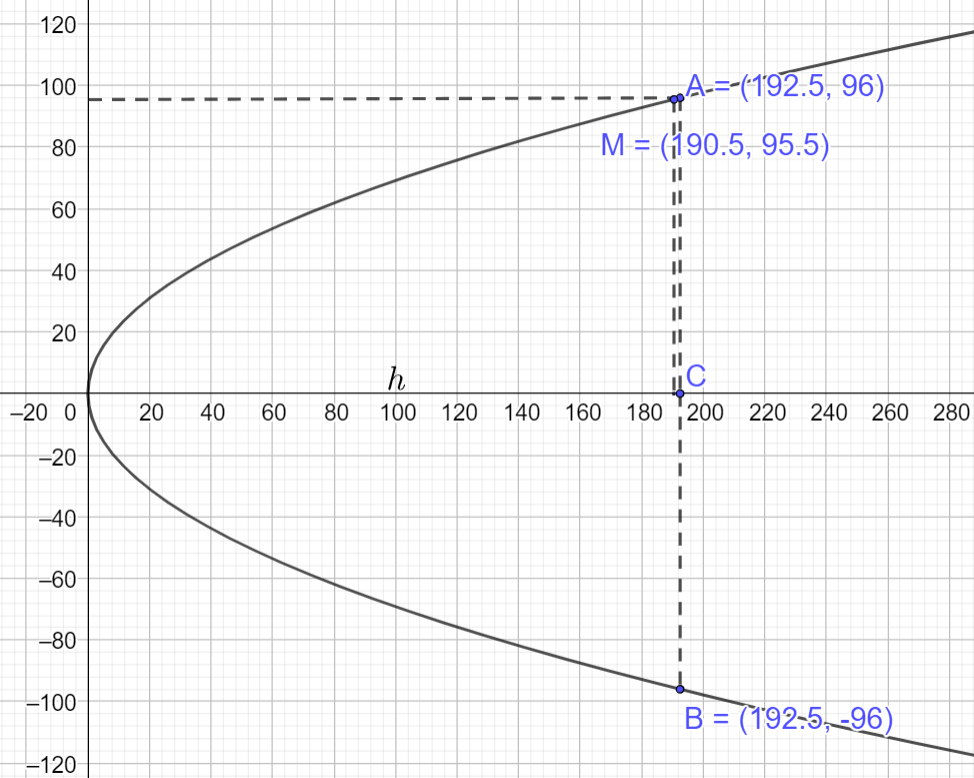
Phương trình parabol mô phỏng cổng có dạng \({y^2} = 2px\)
Theo giả thiết \(AB = 2{y_A} = 192 \Rightarrow {y_A} = 96,OC = h \Rightarrow M\left( {h – 2;95,5} \right),A\left( {h;96} \right)\)
Thay tọa độ các điểm \(M\left( {h – 2;95,5} \right),A\left( {h;96} \right)\) vào phương trình \({y^2} = 2px\) ta có:
\(\left\{ \begin{array}{l}95,{5^2} = 2p\left( {h – 2} \right)\\{96^2} = 2ph\end{array} \right. \Rightarrow \left\{ \begin{array}{l}p = \frac{{383}}{{16}}\\h \simeq 192,5\end{array} \right.\)
Vậy chiều cao của cổng gần bằng 192,5 m