Hướng dẫn giải Luyện tập – Vận dụng 1 Bài 4. Tổng và hiệu của hai vecto (trang 83, 84, 85) – SGK Toán 10 Cánh diều. Hướng dẫn: Bước 1: Chứng minh \(\overrightarrow {PB} = \overrightarrow {NM} ;\;\overrightarrow {AN} = \overrightarrow {NC} \.
Câu hỏi/Đề bài:
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {AN} \)
Hướng dẫn:
Bước 1: Chứng minh \(\overrightarrow {PB} = \overrightarrow {NM} ;\;\overrightarrow {AN} = \overrightarrow {NC} \)
Bước 2: Tính tổng \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {NM} + \overrightarrow {MC} = \overrightarrow {NC} = \overrightarrow {AN} \)
Lời giải:
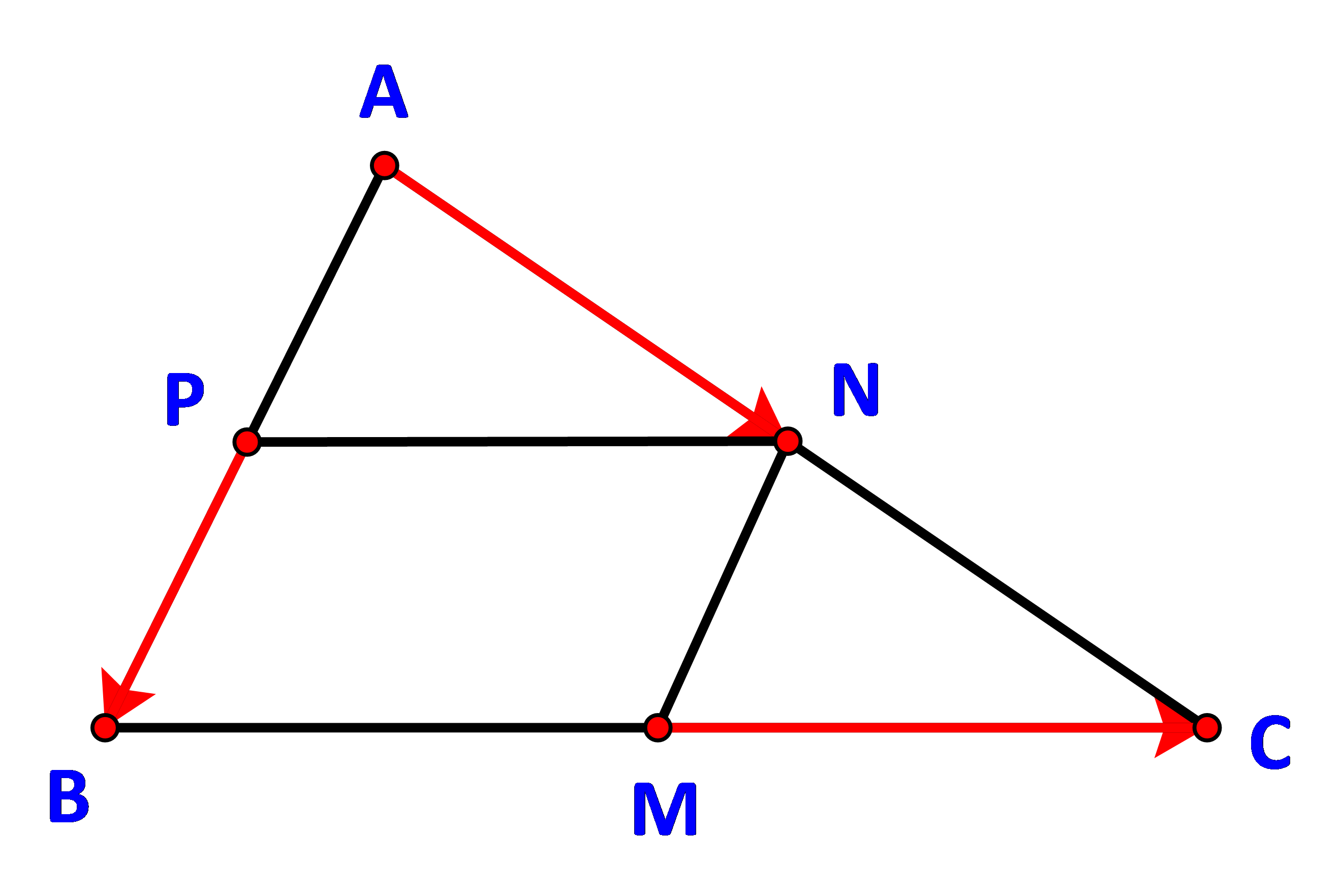
Do M, N, P lần lượt là trung điểm của BC, CA, AB
\( \Rightarrow MN = \frac{{AB}}{2} = PB\) và MN // PB.
\( \Rightarrow \overrightarrow {PB} = \overrightarrow {NM} \)
Ta có: \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {NM} + \overrightarrow {MC} = \overrightarrow {NC} \)
Lại có: \(\overrightarrow {NC} = \overrightarrow {AN} \) (do N là trung điểm của AC)
Vậy \(\overrightarrow {PB} + \overrightarrow {MC} = \overrightarrow {AN} \)