Hướng dẫn giải Hoạt động 4 Bài 3. Phương trình đường thẳng (trang 75, 76) – SGK Toán 10 Cánh diều.
Câu hỏi/Đề bài:
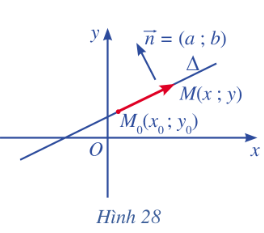
Trong mặt phẳng toạ độ Oxy, cho đường thẳng \(\Delta \) đi qua điểm \({M_o}\left( {{x_o};{y_o}} \right)\) và có vectơ pháp tuyến \(\overrightarrow n {\rm{ }} = \left( {a;{\rm{ }}b} \right)\). Xét điểm M(x ; y) nằm trên \(\Delta \) (Hình 28).
a) Nhận xét về phương của hai vectơ \(\overrightarrow n \) và \(\overrightarrow {{M_o}M} \).
b) Tìm mối liên hệ giữa toạ độ của điểm M với toạ độ của điểm \({M_o}\) và toạ độ của vectơ pháp tuyến \(\overrightarrow n \).
Lời giải:
a) Phương của hai vecto \(\overrightarrow n \) và \(\overrightarrow {{M_o}M} \) vuông góc với nhau.
b) Ta có: \(\overrightarrow {{M_o}M} = \left( {x – {x_o};y – {y_o}} \right),\overrightarrow u = \left( {a;b} \right)\)
Xét điểm \(M\left( {x;y} \right) \in \Delta \). Vì \(\overrightarrow {{M_o}M} \bot \overrightarrow n \) nên: \(\overrightarrow {{M_o}M} .\overrightarrow n = 0 \Leftrightarrow a\left( {x – {x_o}} \right) + b\left( {y – {y_o}} \right) = 0 \Leftrightarrow ax + by – a{x_o} + b{y_o} = 0\)