+) OACB là hình bình hành thì \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \. Hướng dẫn giải Giải bài 9 trang 100 SGK Toán 10 tập 1 – Cánh diều – Bài tập cuối Chương 4. Hai lực F1 ,F2 cho trước cùng tác dụng lên một vật tại điểm O và tạo với nhau một…
Đề bài/câu hỏi:
Hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cho trước cùng tác dụng lên một vật tại điểm O và tạo với nhau một góc \((\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ) = \alpha \) làm cho vật di chuyển theo hướng từ O đến C (Hình 74). Lập công thức tính cường độ của hợp lực \(\overrightarrow F \) làm cho vật di chuyển theo hướng từ O đến C (giả sử chỉ có đúng hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) làm cho vật di chuyển).
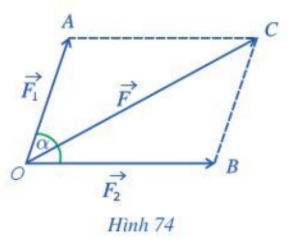
Hướng dẫn:
+) OACB là hình bình hành thì \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \)
+) Tính cường độ của hợp lực \(\overrightarrow F \) bằng định lí cosin: \(O{C^2} = O{A^2} + A{C^2} – 2.OA.AC.\cos A\)
Lời giải:
Ta có: \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\;\overrightarrow {{F_2}} = \overrightarrow {OB}= \overrightarrow {AC} \)
Khi đó: Hợp lực \(\overrightarrow F \) là \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \).
Áp dụng định lí cosin cho tam giác OAC, ta có:
\(\begin{array}{*{20}{l}}{\;\;\;{\mkern 1mu} {\kern 1pt} \;O{C^2} = O{A^2} + A{C^2} – 2.OA.AC.\cos A}\\\begin{array}{l} \Leftrightarrow O{C^2} = O{A^2} + A{C^2} – 2.OA.AC.\cos ({180^o} – \alpha )\\ \Leftrightarrow O{C^2} = O{A^2} + A{C^2} + 2.OA.AC.\cos \alpha \end{array}\\{ \Leftrightarrow \left| {\vec F} \right| = \sqrt {{{\left| {\overrightarrow {{F_1}} } \right|}^2} + {{\left| {\overrightarrow {{F_2}} } \right|}^2} + 2.\left| {\overrightarrow {{F_1}} } \right|.\left| {\overrightarrow {{F_2}} } \right|.\cos \alpha } }\end{array}\)