Xác định vecto tổng (hiệu) rồi tính độ dài. Vận dụng kiến thức giải Giải bài 7 trang 87 SGK Toán 10 tập 1 – Cánh diều – Bài 4. Tổng và hiệu của hai vecto. Cho hình vuông ABCD có cạnh a. Tính độ dài các vecto sau:…
Đề bài/câu hỏi:
Cho hình vuông ABCD có cạnh a. Tính độ dài các vecto sau:
a) \(\overrightarrow {DA} + \overrightarrow {DC} \)
b) \(\overrightarrow {AB} – \overrightarrow {AD} \)
c) \(\overrightarrow {OA} + \overrightarrow {OB} \) với O là giao điểm của AC và BD.
Hướng dẫn:
Xác định vecto tổng (hiệu) rồi tính độ dài.
Lời giải:
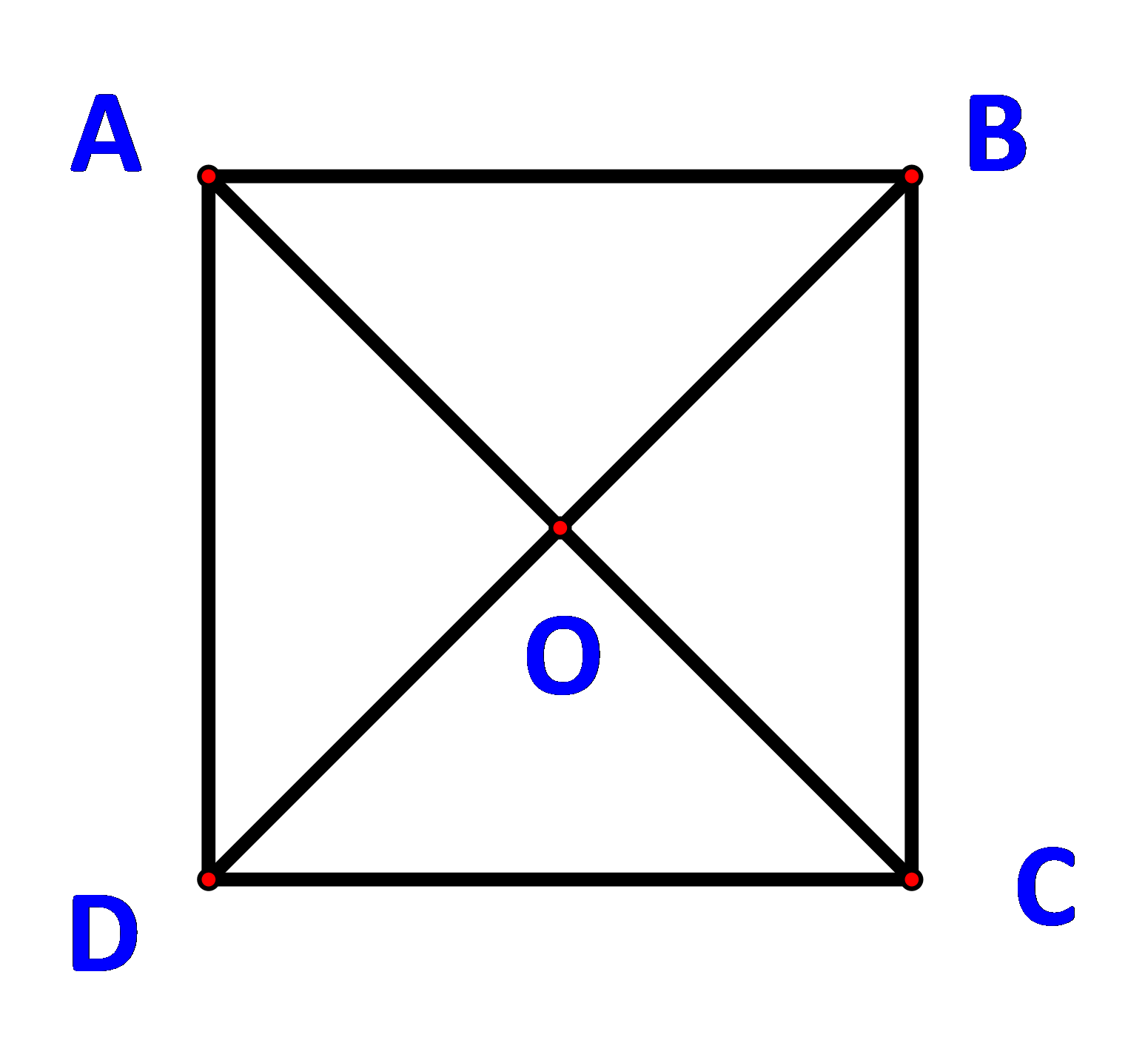
a) Do ABCD cũng là một hình bình hành nên \(\overrightarrow {DA} + \overrightarrow {DC} = \overrightarrow {DB} \)
\( \Rightarrow \;|\overrightarrow {DA} + \overrightarrow {DC} |\; = \;|\overrightarrow {DB} |\; = DB = a\sqrt 2 \)
b) Ta có: \(\overrightarrow {AD} + \overrightarrow {DB} = \overrightarrow {AB} \) \( \Rightarrow \overrightarrow {AB} – \overrightarrow {AD} = \overrightarrow {DB} \)
\( \Rightarrow \left| {\overrightarrow {AB} – \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = DB = a\sqrt 2 \)
c) Ta có: \(\overrightarrow {DO} = \overrightarrow {OB} \)
\( \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {DO} = \overrightarrow {DO} + \overrightarrow {OA} = \overrightarrow {DA} \)
\( \Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {DA} } \right| = DA = a.\)