Bài 5 trang 77 Toán 10 tập 1 – Cánh diều: Tính độ dài cạnh AB trong mỗi trường hợp sau

Đề bài/câu hỏi:

Tính độ dài cạnh AB trong mỗi trường hợp sau:

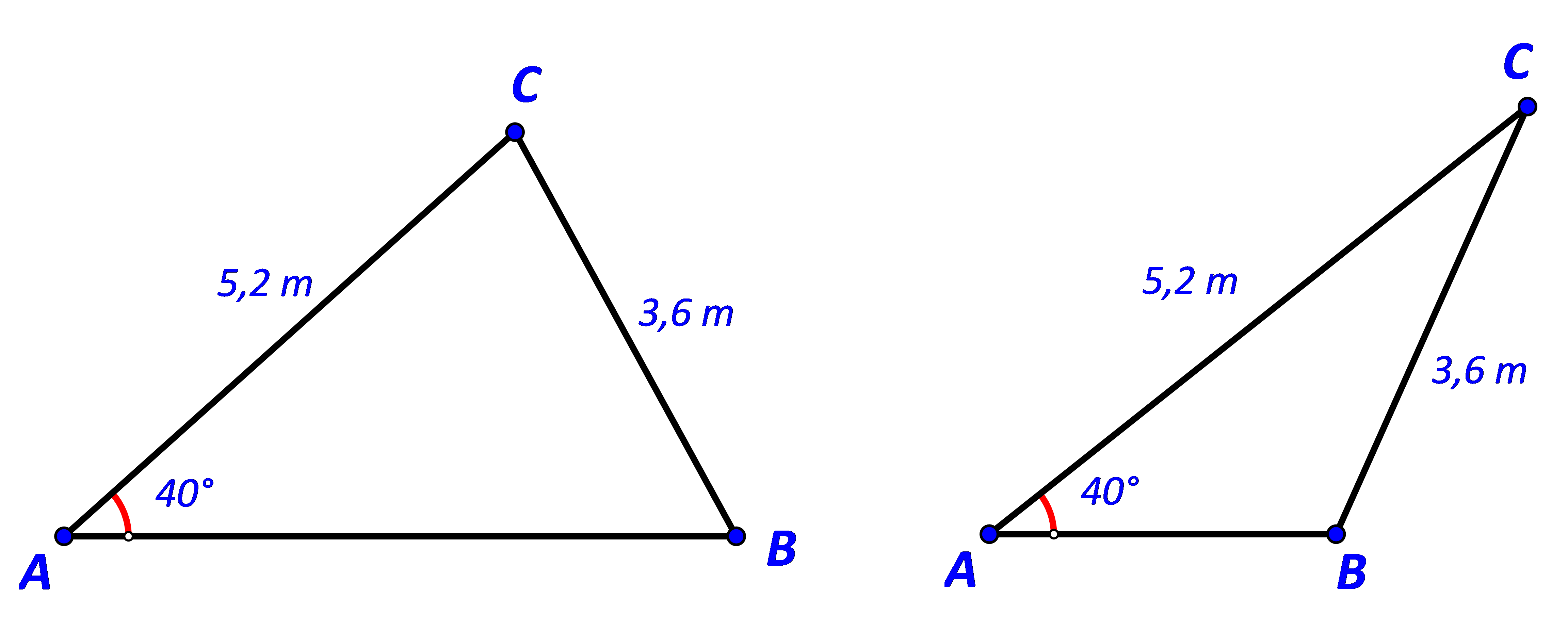
Hướng dẫn:

Bước 1: Tính góc B: Áp dụng định lí sin trong tam giác ABC.

Bước 2: Tính góc C. Áp dụng định lí sin hoặc định lí cosin để tìm AB

Lời giải:

Áp dụng định lí sin trong tam giác ABC, ta có:

\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}}\)

\( \Rightarrow \sin B = \frac{{AC.\sin A}}{{BC}} = \frac{{5,2.\sin {{40}^o}}}{{3,6}} \approx 0,93\)

\( \Rightarrow \widehat B \approx 68,{2^o}\) hoặc \(\widehat B \approx 111,{8^o}\)

Trường hợp 1: (Hình 29) \(\widehat B \approx 68,{2^o}\)

Ta có: \(\widehat C = {180^o} – (\widehat A + \widehat B) = {180^o} – ({40^o} + 68,{2^o}) = 71,{8^o}\)

Áp dụng định lí sin trong tam giác ABC, ta có:

\(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)

\( \Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin 71,{8^o}.\frac{{3,6}}{{\sin {{40}^o}}} \approx 5,32\)

Trường hợp 2: (Hình 30)\(\widehat B \approx 111,{8^o}\)

Ta có: \(\widehat C = {180^o} – (\widehat A + \widehat B) = {180^o} – ({40^o} + 111,{8^o}) = 28,{2^o}\)

Áp dụng định lí sin trong tam giác ABC, ta có:

\(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}\)

\( \Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin 28,{2^o}.\frac{{3,6}}{{\sin {{40}^o}}} \approx 2,65\)

Vậy ở hình 29 thì AB = 5,32m; hình 30 thì AB = 2,65m.