Bài 3 trang 53 Toán 10 tập 2 – Cánh diều: Biểu đồ đoạn thẳng ở Hình 6 cho biết lượng khách du lịch quốc tế đến Việt Nam trong một số năm (từ 1990 đến 2019)

Đề bài/câu hỏi:

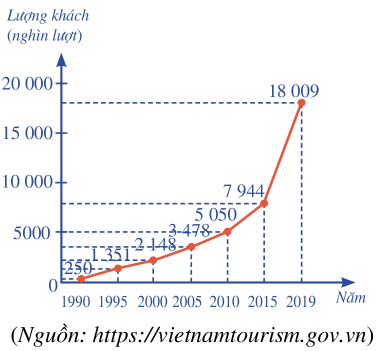
Biểu đồ đoạn thẳng ở Hình 6 cho biết lượng khách du lịch quốc tế đến Việt Nam trong một số năm (từ 1990 đến 2019).

a) Viết mẫu số liệu thống kê số lượt khách du lịch Lượng khách quốc tế đến Việt Nam nhận được từ biểu đồ bên.

b) Viết mẫu số liệu theo thứ tự tăng dần. Tìm số trung bình cộng, trung vị và tứ phân vị của mẫu số liệu đó.

c) Tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó.

d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.

Hướng dẫn:

a) Quan sát biểu đồ

b) Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: \({X_1},{X_2},…,{X_n}\)

Bước 2: Số trung bình cộng : \(\overline x = \frac{{{x_1} + {x_2} + … + {x_n}}}{n}\)

Bước 3: Trung vị \({Q_2} = {M_e} = \left\{ \begin{array}{l}{X_{k + 1}}\quad \quad \quad \quad \quad (n = 2k + 1)\\\frac{1}{2}({X_k} + {X_{k + 1}})\quad \;\,(n = 2k)\end{array} \right.\)

\({Q_1}\) là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)

\({Q_3}\) là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)

c) Khoảng biến thiên: \(R = {X_n} – {X_1}\)

Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} – {Q_1}\)

d) Tính phương sai \({s^2} = \frac{1}{n}\left[ {{{\left( {{x_1} – \overline x } \right)}^2} + {{\left( {{x_2} – \overline x } \right)}^2} + … + {{\left( {{x_n} – \overline x } \right)}^2}} \right]\)

Độ lệch chuẩn \(s = \sqrt {{s^2}} \)

Lời giải:

a) Mẫu số liệu thống kê số lượt khách du lịch Lượng khách quốc tế đến Việt Nam nhận được từ biểu đồ bên là:

250 1351 2148 3478 5050 7944 18009

b) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được: 250 1351 2148 3478 5050 7944 18009

Số trung bình cộng của mẫu số liệu trên là:

\(\overline x = \frac{{250{\rm{ + }}1351{\rm{ + }}2148{\rm{ + }}3478{\rm{ + }}5050{\rm{ + }}7944{\rm{ + }}18009}}{7} = \frac{{38230}}{7}\)

Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 7 số liệu ( lẻ ) nên trung vị \({Q_2} = 3478\)

Tứ phân vị của mẫu số liệu trên là:

– Trung vị của dãy 250 1351 2148 là: \({Q_1} = 1351\)

– Trung vị của dãy 5050 7944 18009 là: \({Q_3} = 7944\)

– Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 1351\), \({Q_2} = 3478\), \({Q_3} = 7944\)

c) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} – {x_{\min }} = 18009 – 250 = 17759\)

Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} – {Q_1} = 7944 – 1351 = 6593\)

d) Phương sai của mẫu số liệu trên là:

\({s^2} = \frac{{\left[ {{{\left( {250 – \overline x } \right)}^2} + {{\left( {351 – \overline x } \right)}^2} + … + {{\left( {18009 – \overline x } \right)}^2}} \right]}}{7} \approx 31820198,82\)

Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 5640,93\)