Vẽ các vecto \(\overrightarrow {OA} = \overrightarrow a , \overrightarrow {OB} = \overrightarrow b , \overrightarrow {OC} = \overrightarrow c . Gợi ý giải Giải bài 1 trang 65 SGK Toán 10 tập 2 – Cánh diều – Bài 1. Tọa độ của vecto. Tìm tọa độ của các vecto trong Hình 16 và biểu diễn mỗi vecto đó qua hai vecto…
Đề bài/câu hỏi:
Tìm tọa độ của các vecto trong Hình 16 và biểu diễn mỗi vecto đó qua hai vecto \(\overrightarrow i , \overrightarrow j \)
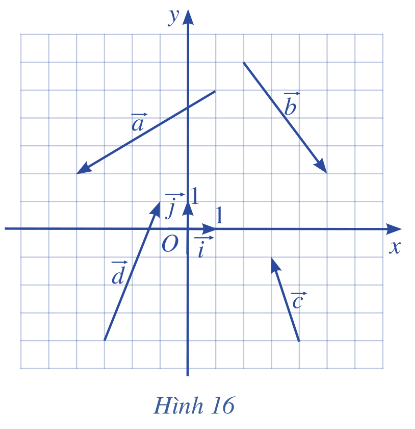
Hướng dẫn:
Vẽ các vecto \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b ,\overrightarrow {OC} = \overrightarrow c ,\overrightarrow {OD} = \overrightarrow d \). Tọa độ của 4 điểm A, B, C, D là tọa độ của 4 vecto.
Để biểu diễn các vecto qua vecto đơn vị: \(\overrightarrow u {\rm{ }} = {\rm{ }}\left( {a;{\rm{ }}b} \right) \Leftrightarrow \overrightarrow u = a\overrightarrow i + b\overrightarrow j \)
Lời giải:
a) Vẽ các vecto \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b ,\overrightarrow {OC} = \overrightarrow c ,\overrightarrow {OD} = \overrightarrow d \)
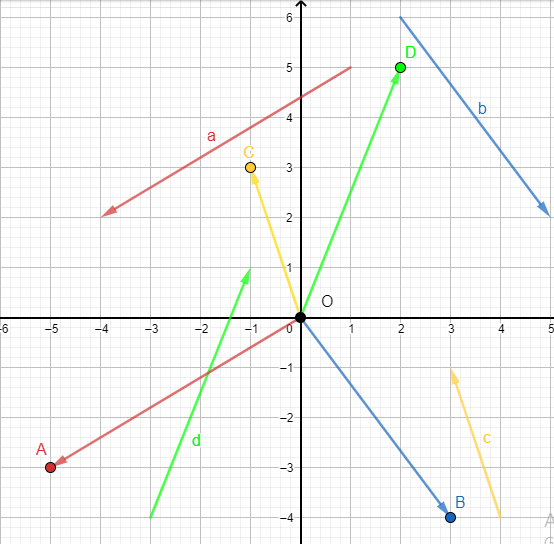
Dựa vào hình vẽ, ta thấy tọa độ của 4 điểm A, B, C, D là:
\(A\left( { – 5; – 3} \right),B\left( {3; – 4} \right),C\left( { – 1;3} \right),D\left( {2;5} \right)\)
Do đó \(\overrightarrow a = \overrightarrow {OA} = \left( { – 5; – 3} \right),\overrightarrow b = \overrightarrow {OB} = \left( {3; – 4} \right),\overrightarrow c = \overrightarrow {OC} = \left( { – 1;3} \right),\overrightarrow d = \overrightarrow {OD} = \left( {2;5} \right)\)
b) Vì \(\overrightarrow a = \overrightarrow {OA} = \left( { – 5; – 3} \right)\)nên \(\overrightarrow a = \left( { – 5} \right)\overrightarrow i + \left( { – 3} \right)\overrightarrow j = – 5\overrightarrow i – 3\overrightarrow j \)
Vì \(\overrightarrow b = \overrightarrow {OB} = \left( {3; – 4} \right)\) nên \(\overrightarrow b = 3\overrightarrow i + \left( { – 4} \right)\overrightarrow j = 3\overrightarrow i – 4\overrightarrow j \)
Vì \(\overrightarrow c = \overrightarrow {OC} = \left( { – 1;3} \right)\) nên \(\overrightarrow c = \left( { – 1} \right)\overrightarrow i + \left( 3 \right)\overrightarrow j = – \overrightarrow i + 3\overrightarrow j \)
Vì \(\overrightarrow d = \overrightarrow {OD} = \left( {2;5} \right)\) nên \(\overrightarrow d = 2\overrightarrow i + 5\overrightarrow j \)